Fit Generalized Kumaraswamy Regression Models

Fits regression models using the Generalized Kumaraswamy (GKw) family of distributions for modeling response variables strictly bounded in the interval (0, 1). The function provides a unified interface for fitting seven nested submodels of the GKw family, allowing flexible modeling of proportions, rates, and other bounded continuous outcomes through regression on distributional parameters.

Maximum Likelihood Estimation is performed via automatic differentiation using the TMB (Template Model Builder) package, ensuring computational efficiency and numerical accuracy. The interface follows standard R regression modeling conventions similar to lm, glm, and betareg, making it immediately familiar to R users.

Usage

gkwreg(
  formula,
  data,
  family = c("gkw", "bkw", "kkw", "ekw", "mc", "kw", "beta"),
  link = NULL,
  link_scale = NULL,
  subset = NULL,
  weights = NULL,
  offset = NULL,
  na.action = getOption("na.action"),
  contrasts = NULL,
  control = gkw_control(),
  model = TRUE,
  x = FALSE,
  y = TRUE,
  ...
)

Arguments

formula

An object of class Formula (or one that can be coerced to that class). The formula uses extended syntax to specify potentially different linear predictors for each distribution parameter:

y ~ model_alpha | model_beta | model_gamma | model_delta | model_lambda

where:

• y is the response variable (must be in the open interval (0, 1))

• model_alpha specifies predictors for the \(\alpha\) parameter

• model_beta specifies predictors for the \(\beta\) parameter

• model_gamma specifies predictors for the \(\gamma\) parameter

• model_delta specifies predictors for the \(\delta\) parameter

• model_lambda specifies predictors for the \(\lambda\) parameter

If a part is omitted or specified as ~ 1, an intercept-only model is used for that parameter. Parts corresponding to fixed parameters (determined by family) are automatically ignored. See Details and Examples for proper usage.

data

A data frame containing the variables specified in formula. Standard R subsetting and missing value handling apply.

family

A character string specifying the distribution family from the Generalized Kumaraswamy hierarchy. Must be one of:

"gkw"

Generalized Kumaraswamy (default). Five parameters: \(\alpha, \beta, \gamma, \delta, \lambda\). Most flexible, suitable when data show complex behavior not captured by simpler families.

"bkw"

Beta-Kumaraswamy. Four parameters: \(\alpha, \beta, \gamma, \delta\) (fixes \(\lambda = 1\)). Combines Beta and Kumaraswamy flexibility.

"kkw"

Kumaraswamy-Kumaraswamy. Four parameters: \(\alpha, \beta, \delta, \lambda\) (fixes \(\gamma = 1\)). Alternative four-parameter generalization.

"ekw"

Exponentiated Kumaraswamy. Three parameters: \(\alpha, \beta, \lambda\) (fixes \(\gamma = 1, \delta = 0\)). Adds flexibility to standard Kumaraswamy.

"mc"

McDonald (Beta Power). Three parameters: \(\gamma, \delta, \lambda\) (fixes \(\alpha = 1, \beta = 1\)). Generalization of Beta distribution.

"kw"

Kumaraswamy. Two parameters: \(\alpha, \beta\) (fixes \(\gamma = 1, \delta = 0, \lambda = 1\)). Computationally efficient alternative to Beta with closed-form CDF.

"beta"

Beta distribution. Two parameters: \(\gamma, \delta\) (fixes \(\alpha = 1, \beta = 1, \lambda = 1\)). Standard choice for proportions and rates, corresponds to shape1 = \(\gamma\), shape2 = \(\delta\).

See Details for guidance on family selection.

link

Link function(s) for the distributional parameters. Can be specified as:

• Single character string: Same link for all relevant parameters. Example: link = "log" applies log link to all parameters.

• Named list: Parameter-specific links for fine control. Example: link = list(alpha = "log", beta = "log", delta = "logit")

Default links (used if link = NULL):

• "log" for \(\alpha, \beta, \gamma, \lambda\) (positive parameters)

• "logit" for \(\delta\) (parameter in (0, 1))

Available link functions:

"log"

Logarithmic link. Maps \((0, \infty) \to (-\infty, \infty)\). Ensures positivity. Most common for shape parameters.

"logit"

Logistic link. Maps \((0, 1) \to (-\infty, \infty)\). Standard for probability-type parameters like \(\delta\).

"probit"

Probit link using normal CDF. Maps \((0, 1) \to (-\infty, \infty)\). Alternative to logit, symmetric tails.

"cloglog"

Complementary log-log. Maps \((0, 1) \to (-\infty, \infty)\). Asymmetric, useful for skewed probabilities.

"cauchy"

Cauchy link using Cauchy CDF. Maps \((0, 1) \to (-\infty, \infty)\). Heavy-tailed alternative to probit.

"identity"

Identity link (no transformation). Use with caution; does not guarantee parameter constraints.

"sqrt"

Square root link. Maps \(x \to \sqrt{x}\). Variance-stabilizing for some contexts.

"inverse"

Inverse link. Maps \(x \to 1/x\). Useful for rate-type parameters.

"inverse-square"

Inverse squared link. Maps \(x \to 1/x^2\).

link_scale

Numeric scale factor(s) controlling the transformation intensity of link functions. Can be:

• Single numeric: Same scale for all parameters.

• Named list: Parameter-specific scales for fine-tuning. Example: link_scale = list(alpha = 10, beta = 10, delta = 1)

Default scales (used if link_scale = NULL):

• 10 for \(\alpha, \beta, \gamma, \lambda\)

• 1 for \(\delta\)

Larger values produce more gradual transformations; smaller values produce more extreme transformations. For probability-type links (logit, probit), smaller scales (e.g., 0.5-2) create steeper response curves, while larger scales (e.g., 5-20) create gentler curves. Adjust if convergence issues arise or if you need different response sensitivities.

subset

Optional vector specifying a subset of observations to be used in fitting. Can be a logical vector, integer indices, or expression evaluating to one of these. Standard R subsetting rules apply.

weights

Optional numeric vector of prior weights (e.g., frequency weights) for observations. Should be non-negative. Currently experimental; use with caution and validate results.

offset

Optional numeric vector or matrix specifying an a priori known component to be included in the linear predictor(s). If a vector, it is applied to the first parameter's predictor. If a matrix, columns correspond to parameters in order (\(\alpha, \beta, \gamma, \delta, \lambda\)). Offsets are added to the linear predictor before applying the link function.

na.action

A function specifying how to handle missing values (NAs). Options include:

na.fail

Stop with error if NAs present (default via getOption("na.action"))

na.omit

Remove observations with NAs

na.exclude

Like na.omit but preserves original length in residuals/fitted values

See na.action for details.

contrasts

Optional list specifying contrasts for factor variables in the model. Format: named list where names are factor variable names and values are contrast specifications. See contrasts and the contrasts.arg argument of model.matrix.

control

A list of control parameters from gkw_control specifying technical details of the fitting process. This includes:

• Optimization algorithm (method)

• Starting values (start)

• Fixed parameters (fixed)

• Convergence tolerances (maxit, reltol, abstol)

• Hessian computation (hessian)

• Verbosity (silent, trace)

Default is gkw_control() which uses sensible defaults for most problems. See gkw_control for complete documentation of all options. Most users never need to modify control parameters.

model

Logical. If TRUE (default), the model frame (data frame containing all variables used in fitting) is returned as component model of the result. Useful for prediction and diagnostics. Set to FALSE to reduce object size.

x

Logical. If TRUE, the list of model matrices (one for each modeled parameter) is returned as component x. Default FALSE. Set to TRUE if you need direct access to design matrices for custom calculations.

y

Logical. If TRUE (default), the response vector (after processing by na.action and subset) is returned as component y. Useful for residual calculations and diagnostics.

...

Additional arguments. Currently used only for backward compatibility with deprecated arguments from earlier versions. Using deprecated arguments triggers informative warnings with migration guidance. Examples of deprecated arguments: plot, conf.level, method, start, fixed, hessian, silent, optimizer.control. These should now be passed via the control argument.

Value

An object of class "gkwreg", which is a list containing the following components. Standard S3 methods are available for this class (see Methods section).

Model Specification:

call

The matched function call

formula

The Formula object used

family

Character string: distribution family used

link

Named list: link functions for each parameter

link_scale

Named list: link scale values for each parameter

param_names

Character vector: names of parameters for this family

fixed_params

Named list: parameters fixed by family definition

control

The gkw_control object used for fitting

Parameter Estimates:

coefficients

Named numeric vector: estimated regression coefficients (on link scale). Names follow the pattern "parameter:predictor", e.g., "alpha:(Intercept)", "alpha:x1", "beta:(Intercept)", "beta:x2".

fitted_parameters

Named list: mean values for each distribution parameter (\(\alpha, \beta, \gamma, \delta, \lambda\)) averaged across all observations

parameter_vectors

Named list: observation-specific parameter values. Contains vectors alphaVec, betaVec, gammaVec, deltaVec, lambdaVec, each of length nobs

Fitted Values and Residuals:

fitted.values

Numeric vector: fitted mean values \(E[Y|X]\) for each observation

residuals

Numeric vector: response residuals (observed - fitted) for each observation

Inference:

vcov

Variance-covariance matrix of coefficient estimates. Only present if control$hessian = TRUE. NULL otherwise.

se

Numeric vector: standard errors of coefficients. Only present if control$hessian = TRUE. NULL otherwise.

Model Fit Statistics:

loglik

Numeric: maximized log-likelihood value

aic

Numeric: Akaike Information Criterion (AIC = -2loglik + 2npar)

bic

Numeric: Bayesian Information Criterion (BIC = -2*loglik + log(nobs)*npar)

deviance

Numeric: deviance (-2 * loglik)

df.residual

Integer: residual degrees of freedom (nobs - npar)

nobs

Integer: number of observations used in fit

npar

Integer: total number of estimated parameters

Diagnostic Statistics:

rmse

Numeric: Root Mean Squared Error of response residuals

efron_r2

Numeric: Efron's pseudo R-squared (1 - SSE/SST, where SSE = sum of squared errors, SST = total sum of squares)

mean_absolute_error

Numeric: Mean Absolute Error of response residuals

Optimization Details:

convergence

Logical: TRUE if optimizer converged successfully, FALSE otherwise

message

Character: convergence message from optimizer

iterations

Integer: number of iterations used by optimizer

method

Character: optimization method used (e.g., "nlminb", "BFGS")

Optional Components (returned if requested via model, x, y):

model

Data frame: the model frame (if model = TRUE)

x

Named list: model matrices for each parameter (if x = TRUE)

y

Numeric vector: the response variable (if y = TRUE)

Internal:

tmb_object

The raw object returned by MakeADFun. Contains the TMB automatic differentiation function and environment. Primarily for internal use and advanced debugging.

Details

Distribution Family Selection

The Generalized Kumaraswamy family provides a flexible hierarchy for modeling bounded responses. Selection should be guided by:

1. Start Simple: Begin with two-parameter families ("kw" or "beta") unless you have strong reasons to use more complex models.

2. Model Comparison: Use information criteria (AIC, BIC) and likelihood ratio tests to compare nested models:

  # Fit sequence of nested models
  fit_kw   <- gkwreg(y ~ x, data, family = "kw")
  fit_ekw  <- gkwreg(y ~ x, data, family = "ekw")
  fit_gkw  <- gkwreg(y ~ x, data, family = "gkw")

  # Compare via AIC
  AIC(fit_kw, fit_ekw, fit_gkw)

  # Formal test (nested models only)
  anova(fit_kw, fit_ekw, fit_gkw)

3. Family Characteristics:

• Beta: Traditional choice, well-understood, good for symmetric or moderately skewed data

• Kumaraswamy (kw): Computationally efficient alternative to Beta, closed-form CDF, similar flexibility

• Exponentiated Kumaraswamy (ekw): Adds flexibility for extreme values and heavy tails

• Beta-Kumaraswamy (bkw), Kumaraswamy-Kumaraswamy (kkw): Four-parameter alternatives when three parameters insufficient

• McDonald (mc): Beta generalization via power parameter, useful for J-shaped distributions

• Kumaraswamy-Kumaraswamy (kkw): Most flexible, use only when simpler families inadequate. It extends kw

• Generalized Kumaraswamy (gkw): Most flexible, use only when simpler families inadequate

4. Avoid Overfitting: More different parameters better model. Use cross-validation or hold-out validation to assess predictive performance.

Formula Specification

The extended formula syntax allows different predictors for each parameter:

Basic Examples:

  # Same predictors for both parameters (two-parameter family)
  y ~ x1 + x2
  # Equivalent to: y ~ x1 + x2 | x1 + x2

  # Different predictors per parameter
  y ~ x1 + x2 | x3 + x4
  # alpha depends on x1, x2
  # beta depends on x3, x4

  # Intercept-only for some parameters
  y ~ x1 | 1
  # alpha depends on x1
  # beta has only intercept

  # Complex specification (five-parameter family)
  y ~ x1 | x2 | x3 | x4 | x5
  # alpha ~ x1, beta ~ x2, gamma ~ x3, delta ~ x4, lambda ~ x5

Important Notes:

• Formula parts correspond to parameters in order: \(\alpha\), \(\beta\), \(\gamma\), \(\delta\), \(\lambda\)

• Unused parts (due to family constraints) are automatically ignored

• Use . to include all predictors: y ~ . | .

• Standard R formula features work: interactions (x1:x2), polynomials (poly(x, 2)), transformations (log(x)), etc.

Link Functions and Scales

Link functions map the range of distributional parameters to the real line, ensuring parameter constraints are satisfied during optimization.

Choosing Links:

• Defaults are usually best: The automatic choices (log for shape parameters, logit for delta) work well in most cases

• Alternative links: Consider if you have theoretical reasons (e.g., probit for latent variable interpretation) or convergence issues

• Identity link: Avoid unless you have constraints elsewhere; can lead to invalid parameter values during optimization

Link Scales: The link_scale parameter controls transformation intensity. Think of it as a "sensitivity" parameter:

• Larger values (e.g., 20): Gentler response to predictor changes

• Smaller values (e.g., 2): Steeper response to predictor changes

• Default (10): Balanced, works well for most cases

Adjust only if:

• Convergence difficulties arise

• You need very steep or very gentle response curves

• Predictors have unusual scales (very large or very small)

Optimization and Convergence

The default optimizer (method = "nlminb") works well for most problems. If convergence issues occur:

1. Check Data:

• Ensure response is strictly in (0, 1)

• Check for extreme outliers or influential points

• Verify predictors aren't perfectly collinear

• Consider rescaling predictors to similar ranges

2. Try Alternative Optimizers:

  # BFGS often more robust for difficult problems
  fit <- gkwreg(y ~ x, data,
                control = gkw_control(method = "BFGS"))

  # Nelder-Mead for non-smooth objectives
  fit <- gkwreg(y ~ x, data,
                control = gkw_control(method = "Nelder-Mead"))

3. Adjust Tolerances:

  # Increase iterations and loosen tolerance
  fit <- gkwreg(y ~ x, data,
                control = gkw_control(maxit = 1000, reltol = 1e-6))

4. Provide Starting Values:

  # Fit simpler model first, use as starting values
  fit_simple <- gkwreg(y ~ 1, data, family = "kw")
  start_vals <- list(
    alpha = c(coef(fit_simple)[1], rep(0, ncol(X_alpha) - 1)),
    beta  = c(coef(fit_simple)[2], rep(0, ncol(X_beta) - 1))
  )
  fit_complex <- gkwreg(y ~ x1 + x2 | x3 + x4, data, family = "kw",
                         control = gkw_control(start = start_vals))

5. Simplify Model:

• Use simpler family (e.g., "kw" instead of "gkw")

• Reduce number of predictors

• Use intercept-only for some parameters

Standard Errors and Inference

By default, standard errors are computed via the Hessian matrix at the MLE. This provides valid asymptotic standard errors under standard regularity conditions.

When Standard Errors May Be Unreliable:

• Small sample sizes (n < 30-50 per parameter)

• Parameters near boundaries

• Highly collinear predictors

• Mis-specified models

Alternatives:

• Bootstrap confidence intervals (more robust, computationally expensive)

• Profile likelihood intervals via confint(..., type = "profile") (not yet implemented)

• Cross-validation for predictive performance assessment

To skip Hessian computation (faster, no SEs):

  fit <- gkwreg(y ~ x, data,
                control = gkw_control(hessian = FALSE))

Model Diagnostics

Always check model adequacy using diagnostic plots:

  fit <- gkwreg(y ~ x, data, family = "kw")
  plot(fit)  # Six diagnostic plots

Key diagnostics:

• Residual plots: Check for patterns, heteroscedasticity

• Half-normal plot: Assess distributional adequacy

• Cook's distance: Identify influential observations

• Predicted vs observed: Overall fit quality

See plot.gkwreg for detailed interpretation guidance.

Computational Considerations

Performance Tips:

• GKw family: Most computationally expensive (~2-5x slower than kw/beta)

• Beta/Kw families: Fastest, use when adequate

• Large datasets (n > 10,000): Consider sampling for exploratory analysis

• TMB uses automatic differentiation: Fast gradient/Hessian computation

• Disable Hessian (hessian = FALSE) for faster fitting without SEs

Memory Usage:

• Set model = FALSE, x = FALSE, y = FALSE to reduce object size (but limits some post-fitting capabilities)

• Hessian matrix scales as O(p²) where p = number of parameters

Methods

The following S3 methods are available for objects of class "gkwreg":

Basic Methods:

• print.gkwreg: Print basic model information

• summary.gkwreg: Detailed model summary with coefficient tables, tests, and fit statistics

• coef.gkwreg: Extract coefficients

• vcov.gkwreg: Extract variance-covariance matrix

• logLik: Extract log-likelihood

• AIC, BIC: Information criteria

Prediction and Fitted Values:

• fitted.gkwreg: Extract fitted values

• residuals.gkwreg: Extract residuals (multiple types available)

• predict.gkwreg: Predict on new data

Inference:

• confint.gkwreg: Confidence intervals for parameters

• anova.gkwreg: Compare nested models via likelihood ratio tests

Diagnostics:

• plot.gkwreg: Comprehensive diagnostic plots (6 types)

References

Generalized Kumaraswamy Distribution:

Cordeiro, G. M., & de Castro, M. (2011). A new family of generalized distributions. Journal of Statistical Computation and Simulation, 81(7), 883-898. doi:10.1080/00949650903530745

Kumaraswamy Distribution:

Kumaraswamy, P. (1980). A generalized probability density function for double-bounded random processes. Journal of Hydrology, 46(1-2), 79-88. doi:10.1016/0022-1694(80)90036-0

Jones, M. C. (2009). Kumaraswamy's distribution: A beta-type distribution with some tractability advantages. Statistical Methodology, 6(1), 70-81. doi:10.1016/j.stamet.2008.04.001

Beta Regression:

Ferrari, S. L. P., & Cribari-Neto, F. (2004). Beta regression for modelling rates and proportions. Journal of Applied Statistics, 31(7), 799-815. doi:10.1080/0266476042000214501

Smithson, M., & Verkuilen, J. (2006). A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychological Methods, 11(1), 54-71. doi:10.1037/1082-989X.11.1.54

Template Model Builder (TMB):

Kristensen, K., Nielsen, A., Berg, C. W., Skaug, H., & Bell, B. M. (2016). TMB: Automatic Differentiation and Laplace Approximation. Journal of Statistical Software, 70(5), 1-21. doi:10.18637/jss.v070.i05

Related Software:

Zeileis, A., & Croissant, Y. (2010). Extended Model Formulas in R: Multiple Parts and Multiple Responses. Journal of Statistical Software, 34(1), 1-13. doi:10.18637/jss.v034.i01

See also

Control and Inference: gkw_control for fitting control parameters, confint.gkwreg for confidence intervals, anova.gkwreg for model comparison

Methods: summary.gkwreg, plot.gkwreg, coef.gkwreg, vcov.gkwreg, fitted.gkwreg, residuals.gkwreg, predict.gkwreg

Distributions: dgkw, pgkw, qgkw, rgkw for the GKw distribution family functions

Related Packages: betareg for traditional beta regression, Formula for extended formula interface, MakeADFun for TMB functionality

Author

Lopes, J. E.

Maintainer: Lopes, J. E.

Examples

# \donttest{
# SECTION 1: Basic Usage - Getting Started
# Load packages and data
library(gkwreg)
library(gkwdist)
data(GasolineYield)

# Example 1.1: Simplest possible model (intercept-only, all defaults)
fit_basic <- gkwreg(yield ~ 1, data = GasolineYield, family = "kw")
summary(fit_basic)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: kw 
#> 
#> Call:
#> gkwreg(formula = yield ~ 1, data = GasolineYield, family = "kw")
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.1688 -0.0803 -0.0188 -0.0002  0.0737  0.2602 
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> alpha:(Intercept)   0.6342     0.1538   4.124 3.73e-05 ***
#> beta:(Intercept)    2.7951     0.4319   6.472 9.68e-11 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                       3%    98%
#> alpha:(Intercept) 0.3328 0.9356
#> beta:(Intercept)  1.9486 3.6416
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> 
#> Fitted parameter means:
#> alpha: 1.886
#> beta: 16.35
#> gamma: 1
#> delta: 0
#> lambda: 1
#> 
#> Model fit statistics:
#> Number of observations: 32 
#> Number of parameters: 2 
#> Residual degrees of freedom: 30 
#> Log-likelihood: 28.51 
#> AIC: -53.02 
#> BIC: -50.09 
#> RMSE: 0.1055 
#> Efron's R2: -4.747e-06 
#> Mean Absolute Error: 0.09088 
#> 
#> Convergence status: Successful 
#> Iterations: 11 
#> 

# Example 1.2: Model with predictors (uses all defaults)
# Default: family = "gkw", method = "nlminb", hessian = TRUE
fit_default <- gkwreg(yield ~ batch + temp, data = GasolineYield)
summary(fit_default)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: gkw 
#> 
#> Call:
#> gkwreg(formula = yield ~ batch + temp, data = GasolineYield)
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.0272 -0.0123 -0.0010 -0.0013  0.0079  0.0268 
#> 
#> Coefficients:
#>                      Estimate Std. Error  z value Pr(>|z|)    
#> alpha:(Intercept)  -3.381e+00  7.662e-01   -4.413 1.02e-05 ***
#> alpha:batch1        9.204e-01  3.181e-02   28.930  < 2e-16 ***
#> alpha:batch2        6.787e-01  3.407e-02   19.922  < 2e-16 ***
#> alpha:batch3        7.832e-01  3.400e-02   23.039  < 2e-16 ***
#> alpha:batch4        5.598e-01  3.185e-02   17.573  < 2e-16 ***
#> alpha:batch5        5.632e-01  3.396e-02   16.582  < 2e-16 ***
#> alpha:batch6        5.419e-01  3.403e-02   15.923  < 2e-16 ***
#> alpha:batch7        3.113e-01  3.188e-02    9.767  < 2e-16 ***
#> alpha:batch8        2.549e-01  3.394e-02    7.510 5.91e-14 ***
#> alpha:batch9        1.990e-01  3.794e-02    5.246 1.55e-07 ***
#> alpha:temp          5.408e-03  1.456e-06 3715.029  < 2e-16 ***
#> beta:(Intercept)    2.622e+00  3.722e-01    7.043 1.88e-12 ***
#> gamma:(Intercept)   2.261e+01  1.831e+00   12.346  < 2e-16 ***
#> delta:(Intercept)  -1.457e-01  1.217e+00   -0.120    0.905    
#> lambda:(Intercept) -9.556e+00  4.202e+00   -2.274    0.023 *  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                          3%     98%
#> alpha:(Intercept)   -4.8831 -1.8795
#> alpha:batch1         0.8581  0.9828
#> alpha:batch2         0.6120  0.7455
#> alpha:batch3         0.7166  0.8499
#> alpha:batch4         0.4973  0.6222
#> alpha:batch5         0.4966  0.6298
#> alpha:batch6         0.4752  0.6085
#> alpha:batch7         0.2488  0.3738
#> alpha:batch8         0.1884  0.3215
#> alpha:batch9         0.1247  0.2734
#> alpha:temp           0.0054  0.0054
#> beta:(Intercept)     1.8922  3.3513
#> gamma:(Intercept)   19.0207 26.1992
#> delta:(Intercept)   -2.5311  2.2397
#> lambda:(Intercept) -17.7927 -1.3201
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> gamma: log
#> delta: logit
#> lambda: log
#> 
#> Fitted parameter means:
#> alpha: 0.3603
#> beta: 13.76
#> gamma: 6.598e+09
#> delta: 4.636
#> lambda: 7.068e-05
#> 
#> Model fit statistics:
#> Number of observations: 32 
#> Number of parameters: 15 
#> Residual degrees of freedom: 17 
#> Log-likelihood: 96.5 
#> AIC: -163 
#> BIC: -141 
#> RMSE: 0.01406 
#> Efron's R2: 0.9822 
#> Mean Absolute Error: 0.01129 
#> 
#> Convergence status: Failed 
#> Iterations: 146 
#> 

# Example 1.3: Kumaraswamy model (two-parameter family)
# Default link functions: log for both alpha and beta
fit_kw <- gkwreg(yield ~ batch + temp, data = GasolineYield, family = "kw")
#> Warning: NaNs produced
summary(fit_kw)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: kw 
#> 
#> Call:
#> gkwreg(formula = yield ~ batch + temp, data = GasolineYield, 
#>     family = "kw")
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.0307 -0.0074  0.0036 -0.0007  0.0086  0.0175 
#> 
#> Coefficients:
#>                    Estimate Std. Error z value Pr(>|z|)    
#> alpha:(Intercept)  0.669333   0.028696  23.325  < 2e-16 ***
#> alpha:batch1       0.838133   0.026691  31.401  < 2e-16 ***
#> alpha:batch2       0.591261   0.028544  20.714  < 2e-16 ***
#> alpha:batch3       0.710279   0.028476  24.943  < 2e-16 ***
#> alpha:batch4       0.466760   0.026679  17.496  < 2e-16 ***
#> alpha:batch5       0.520279   0.028409  18.314  < 2e-16 ***
#> alpha:batch6       0.449768   0.028512  15.775  < 2e-16 ***
#> alpha:batch7       0.224772   0.026625   8.442  < 2e-16 ***
#> alpha:batch8       0.203167   0.028283   7.183 6.80e-13 ***
#> alpha:batch9       0.141873   0.031899   4.448 8.69e-06 ***
#> alpha:temp         0.005282        NaN     NaN      NaN    
#> beta:(Intercept)  28.881137   0.430082  67.153  < 2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                        3%     98%
#> alpha:(Intercept)  0.6131  0.7256
#> alpha:batch1       0.7858  0.8904
#> alpha:batch2       0.5353  0.6472
#> alpha:batch3       0.6545  0.7661
#> alpha:batch4       0.4145  0.5190
#> alpha:batch5       0.4646  0.5760
#> alpha:batch6       0.3939  0.5056
#> alpha:batch7       0.1726  0.2770
#> alpha:batch8       0.1477  0.2586
#> alpha:batch9       0.0794  0.2044
#> alpha:temp            NaN     NaN
#> beta:(Intercept)  28.0382 29.7241
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> 
#> Fitted parameter means:
#> alpha: 18.47
#> beta: 3.487e+12
#> gamma: 1
#> delta: 0
#> lambda: 1
#> 
#> Model fit statistics:
#> Number of observations: 32 
#> Number of parameters: 12 
#> Residual degrees of freedom: 20 
#> Log-likelihood: 96.97 
#> AIC: -169.9 
#> BIC: -152.3 
#> RMSE: 0.01292 
#> Efron's R2: 0.985 
#> Mean Absolute Error: 0.01068 
#> 
#> Convergence status: Failed 
#> Iterations: 77 
#> 

par(mfrow = c(3, 2))
plot(fit_kw, ask = FALSE)
#> Simulating envelope ( 100 iterations): .......... Done!


# Example 1.4: Beta model for comparison
# Default links: log for gamma and delta
fit_beta <- gkwreg(yield ~ batch + temp, data = GasolineYield, family = "beta")
#> using C++ compiler: ‘g++ (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’

# Compare models using AIC/BIC
AIC(fit_kw, fit_beta)
#>          df        AIC
#> fit_kw   12 -169.93865
#> fit_beta 12  -66.52315
BIC(fit_kw, fit_beta)
#>          df        BIC
#> fit_kw   12 -152.34982
#> fit_beta 12  -48.93432

# SECTION 2: Using gkw_control() for Customization

# Example 2.1: Change optimization method to BFGS
fit_bfgs <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  control = gkw_control(method = "BFGS")
)
summary(fit_bfgs)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: kw 
#> 
#> Call:
#> gkwreg(formula = yield ~ batch + temp, data = GasolineYield, 
#>     family = "kw", control = gkw_control(method = "BFGS"))
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.4270 -0.3404 -0.2601 -0.2400 -0.1571  0.0346 
#> 
#> Coefficients:
#>                     Estimate Std. Error z value Pr(>|z|)
#> alpha:(Intercept) -2.642e-06  1.244e+00   0.000    1.000
#> alpha:batch1      -1.481e-07  7.956e-01   0.000    1.000
#> alpha:batch2      -2.952e-07  7.610e-01   0.000    1.000
#> alpha:batch3      -2.558e-07  7.878e-01   0.000    1.000
#> alpha:batch4      -3.067e-07  6.980e-01   0.000    1.000
#> alpha:batch5      -1.339e-07  7.555e-01   0.000    1.000
#> alpha:batch6      -1.890e-07  7.388e-01   0.000    1.000
#> alpha:batch7      -5.561e-07  6.586e-01   0.000    1.000
#> alpha:batch8      -2.938e-07  6.854e-01   0.000    1.000
#> alpha:batch9      -1.461e-07  7.854e-01   0.000    1.000
#> alpha:temp        -7.717e-04  3.133e-03  -0.246    0.805
#> beta:(Intercept)   2.530e-06  5.131e-01   0.000    1.000
#> 
#> Confidence intervals (95%):
#>                        3%    98%
#> alpha:(Intercept) -2.4382 2.4382
#> alpha:batch1      -1.5593 1.5593
#> alpha:batch2      -1.4916 1.4916
#> alpha:batch3      -1.5441 1.5441
#> alpha:batch4      -1.3680 1.3680
#> alpha:batch5      -1.4808 1.4808
#> alpha:batch6      -1.4479 1.4479
#> alpha:batch7      -1.2908 1.2908
#> alpha:batch8      -1.3433 1.3433
#> alpha:batch9      -1.5394 1.5394
#> alpha:temp        -0.0069 0.0054
#> beta:(Intercept)  -1.0057 1.0057
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> 
#> Fitted parameter means:
#> alpha: 0.775
#> beta: 0.999
#> gamma: 1
#> delta: 0
#> lambda: 1
#> 
#> Model fit statistics:
#> Number of observations: 32 
#> Number of parameters: 12 
#> Residual degrees of freedom: 20 
#> Log-likelihood: 4.18 
#> AIC: 15.64 
#> BIC: 33.23 
#> RMSE: 0.2662 
#> Efron's R2: -5.362 
#> Mean Absolute Error: 0.2422 
#> 
#> Convergence status: Successful 
#> Iterations: 12 
#> 

# Example 2.2: Increase iterations and enable verbose output
fit_verbose <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  control = gkw_control(
    method = "nlminb",
    maxit = 1000,
    silent = FALSE, # Show optimization progress
    trace = 1 # Print iteration details
  )
)
#> Using TMB model: kwreg
#> [TMB] Preparing TMB model: kwreg
#> [TMB] Loaded DLL: kwreg.so
#> [TMB] Loaded cached DLL: kwreg
#> Optimizing with nlminb...
#> outer mgc:  7535.888 
#>   0:     0.0000000:  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000  0.00000
#> outer mgc:  1043.999 
#>   1:    -5.4751175: -4.63847e-06 -2.59943e-07 -5.18250e-07 -4.49143e-07 -5.38512e-07 -2.35055e-07 -3.31849e-07 -9.76418e-07 -5.15872e-07 -2.56583e-07 -0.00135487 4.44139e-06
#> outer mgc:  248.2347 
#>   2:    -5.6372510: -0.000220415 4.16287e-05 -6.57121e-05 -4.96481e-05 -2.17994e-05 4.41064e-05 1.14631e-05 -0.000146966 -2.99241e-05 1.37058e-05 -0.00157060 0.00131183
#> outer mgc:  473.1837 
#>   3:    -17.969328: -0.136724 0.0277276 -0.0411281 -0.0307797 -0.0132258 0.0285480 0.00773975 -0.0933782 -0.0190868 0.00856339 0.000220983 0.807421
#> outer mgc:  9403.659 
#>   4:    -26.755529: -1.05462 0.724290 -0.0972976 0.0815258 -0.00801223 0.221600 0.0531230 -0.597665 -0.396572 -0.204538 0.00463826  1.75768
#> outer mgc:  2886.778 
#>   5:    -37.161577: -1.99422 0.532895 0.375388 0.595205 0.184898 0.118380 0.0752171 0.0400090 -0.446348 -0.559931 0.00739496  2.61648
#> outer mgc:  7.749627 
#>   6:    -37.319116: -1.99422 0.532895 0.375388 0.595205 0.184898 0.118380 0.0752172 0.0400089 -0.446347 -0.559931 0.00728617  2.61648
#> outer mgc:  550.0578 
#>   7:    -41.464061: -2.02667 0.914794  1.02259 0.900567 0.498035 0.229685 0.432451 0.250005 0.606057 -0.140198 0.00692665  3.32846
#> outer mgc:  5344.69 
#>   8:    -45.753042: -1.76430  1.27538  1.24545  1.16880 0.977965 0.907505 0.936306 0.774485  1.02539 0.611458 0.00552332  4.00061
#> outer mgc:  1670.43 
#>   9:    -47.955163: -1.64864  1.22488  1.11887  1.24717 0.859116 0.813747 0.957285 0.611050 0.863210 0.747015 0.00532993  4.07981
#> outer mgc:  9795.288 
#>  10:    -51.767663: -1.40959  1.20843 0.839361 0.870775 0.757785 0.725397 0.685794 0.396577 0.539655 0.627278 0.00501252  4.22953
#> outer mgc:  2710.496 
#>  11:    -53.248253: -1.12767  1.06051 0.668602 0.815387 0.477102 0.862767 0.718959 0.248646 0.338869 0.171931 0.00481642  4.46311
#> outer mgc:  16842.91 
#>  12:    -53.429246: -1.03560 0.930350 0.552767 0.812949 0.558985 0.739392 0.653578 0.201404 0.199360 0.0828970 0.00510502  4.64797
#> outer mgc:  1617.054 
#>  13:    -56.920478: -1.04556 0.887457 0.544651 0.761934 0.449875 0.698924 0.597230 0.252503 0.149860 0.124954 0.00497747  4.71163
#> outer mgc:  2975.096 
#>  14:    -57.122716: -1.05628 0.887144 0.621162 0.746286 0.377752 0.704226 0.517575 0.263577 0.114298 0.184229 0.00515212  4.80920
#> outer mgc:  5629.443 
#>  15:    -59.508340: -1.16932 0.831867 0.647262 0.740311 0.473678 0.698786 0.442163 0.126740 0.190201 0.212037 0.00583191  5.38867
#> outer mgc:  4395.124 
#>  16:    -63.076455: -1.15522 0.976613 0.645814 0.760813 0.523103 0.518533 0.436436 0.149771 0.199569 0.171118 0.00602373  5.96632
#> outer mgc:  196.8215 
#>  17:    -63.160743: -1.15522 0.976613 0.645814 0.760813 0.523103 0.518533 0.436436 0.149771 0.199569 0.171118 0.00598723  5.96632
#> outer mgc:  18.42406 
#>  18:    -63.161178: -1.15521 0.976604 0.645809 0.760798 0.523100 0.518521 0.436445 0.149773 0.199566 0.171117 0.00598550  5.96635
#> outer mgc:  461.7689 
#>  19:    -63.890234: -1.12318 0.928341 0.620142 0.679521 0.504704 0.446154 0.489708 0.158607 0.181216 0.166103 0.00601617  6.12062
#> outer mgc:  791.2478 
#>  20:    -66.036596: -0.800206 0.769772 0.518142 0.643273 0.495658 0.295760 0.349990 0.156598 0.120672 0.0735364 0.00553780  6.68285
#> outer mgc:  8171.629 
#>  21:    -69.640060: -0.668180 0.830978 0.522586 0.674831 0.529395 0.393655 0.415273 0.236722 0.179303 0.125246 0.00532357  7.36258
#> outer mgc:  1565.565 
#>  22:    -70.355079: -0.626741 0.844078 0.585063 0.678075 0.561437 0.412512 0.448970 0.234407 0.160557 0.127507 0.00518349  7.51316
#> outer mgc:  16132.41 
#>  23:    -70.925305: -0.656731 0.855902 0.591969 0.712135 0.557942 0.437277 0.462929 0.267301 0.186961 0.131086 0.00519836  7.67594
#> outer mgc:  992.5871 
#>  24:    -72.287011: -0.656650 0.866594 0.616989 0.732895 0.565204 0.457702 0.481938 0.284546 0.196027 0.134163 0.00530147  7.84613
#> outer mgc:  10629.38 
#>  25:    -75.105520: -0.494803 0.937004 0.806321 0.861938 0.579462 0.628636 0.624693 0.384401 0.289508 0.186246 0.00521692  9.70792
#> outer mgc:  18969.12 
#>  26:    -76.692255: -0.333361 0.887587 0.734577 0.783233 0.508464 0.600339 0.566039 0.306909 0.258688 0.197094 0.00500158  10.0584
#> outer mgc:  6260.027 
#>  27:    -79.259103: -0.369687 0.862439 0.670965 0.759088 0.497862 0.596401 0.509338 0.276911 0.163088 0.176222 0.00526577  10.4567
#> outer mgc:  16287.87 
#>  28:    -81.053798: -0.376928 0.870388 0.626177 0.705981 0.497203 0.570252 0.452039 0.237364 0.224924 0.150962 0.00537596  10.8617
#> outer mgc:  12963.16 
#>  29:    -82.151851: -0.364627 0.880116 0.606015 0.722805 0.507469 0.549036 0.458418 0.233001 0.224630 0.156515 0.00551800  11.2830
#> outer mgc:  8317.292 
#>  30:    -83.329837: -0.312697 0.874169 0.594294 0.739479 0.490313 0.514716 0.475484 0.229621 0.224870 0.172911 0.00546802  11.6999
#> outer mgc:  16486.14 
#>  31:    -84.986835: -0.192865 0.853400 0.595130 0.717311 0.477081 0.490337 0.460508 0.235518 0.216189 0.162595 0.00536386  12.5363
#> outer mgc:  16178.4 
#>  32:    -86.555130: -0.103660 0.852072 0.593116 0.723514 0.494456 0.507035 0.475202 0.234153 0.220827 0.171784 0.00526956  13.3773
#> outer mgc:  29858.1 
#>  33:    -88.596572: -0.0142778 0.872344 0.620063 0.744182 0.474163 0.523267 0.479167 0.257521 0.213986 0.146453 0.00535175  15.0663
#> outer mgc:  4090.948 
#>  34:    -88.615340: -0.000990117 0.902580 0.704435 0.787394 0.558575 0.568736 0.517017 0.339891 0.253565 0.244840 0.00543371  16.7473
#> outer mgc:  6187 
#>  35:    -90.392361: 0.0985384 0.859188 0.666724 0.747058 0.538160 0.535854 0.494613 0.299087 0.221230 0.165105 0.00537535  17.5781
#> outer mgc:  23677.04 
#>  36:    -90.601186: 0.285604 0.888612 0.601393 0.700915 0.510188 0.513569 0.451882 0.236701 0.192324 0.123306 0.00521226  19.2551
#> outer mgc:  5588.837 
#>  37:    -92.504039: 0.314495 0.858162 0.577322 0.696464 0.473482 0.521344 0.444638 0.208070 0.197319 0.121994 0.00516530  19.3876
#> outer mgc:  3309.009 
#>  38:    -93.042485: 0.316922 0.850751 0.574503 0.695607 0.469865 0.519612 0.445518 0.208463 0.198603 0.125129 0.00518065  19.5362
#> outer mgc:  3996.36 
#>  39:    -93.550654: 0.320696 0.843080 0.584565 0.705608 0.469072 0.517989 0.444761 0.205085 0.200705 0.126715 0.00520644  19.8338
#> outer mgc:  17352.89 
#>  40:    -93.849295: 0.332284 0.837333 0.584783 0.707135 0.467210 0.521063 0.448395 0.208314 0.202877 0.128243 0.00522856  20.1314
#> outer mgc:  3406.956 
#>  41:    -94.407020: 0.332577 0.839173 0.587505 0.710933 0.467005 0.525668 0.458377 0.222651 0.205102 0.130060 0.00524213  20.4289
#> outer mgc:  3404.857 
#>  42:    -94.965671: 0.338916 0.840802 0.596147 0.710362 0.473493 0.511103 0.456749 0.226911 0.203994 0.151337 0.00533729  21.2777
#> outer mgc:  11746.01 
#>  43:    -95.316481: 0.385958 0.835928 0.593772 0.718096 0.472879 0.514803 0.454766 0.233790 0.209386 0.152955 0.00531950  22.1256
#> outer mgc:  29124.99 
#>  44:    -95.424086: 0.420780 0.842717 0.608497 0.718265 0.475043 0.523533 0.473657 0.236527 0.216088 0.158017 0.00532031  22.9738
#> outer mgc:  26417.85 
#>  45:    -95.903344: 0.450111 0.857226 0.610561 0.733603 0.486468 0.535142 0.464887 0.241711 0.218040 0.154498 0.00532283  23.8222
#> outer mgc:  7281.973 
#>  46:    -96.130130: 0.482702 0.846683 0.602675 0.722989 0.477554 0.529472 0.454392 0.235030 0.210302 0.152475 0.00525428  24.0048
#> outer mgc:  494.6355 
#>  47:    -96.419388: 0.517818 0.839957 0.588196 0.712568 0.469754 0.516728 0.450185 0.224012 0.204822 0.138567 0.00526935  24.7520
#> outer mgc:  15964.68 
#>  48:    -96.538002: 0.550105 0.835039 0.586860 0.706279 0.466407 0.518103 0.446995 0.221504 0.199669 0.138062 0.00527778  25.4999
#> outer mgc:  15028.28 
#>  49:    -96.659094: 0.557183 0.845174 0.599214 0.713727 0.475068 0.523387 0.461330 0.230087 0.209579 0.142691 0.00531772  26.2480
#> outer mgc:  13673.4 
#>  50:    -96.710876: 0.582408 0.845663 0.596602 0.717699 0.467337 0.516888 0.457807 0.228836 0.201827 0.146314 0.00530960  26.7750
#> outer mgc:  16619.74 
#>  51:    -96.746241: 0.612360 0.835150 0.589210 0.710122 0.466433 0.522171 0.443317 0.223072 0.203398 0.146455 0.00526606  27.1802
#> outer mgc:  3054.736 
#>  52:    -96.856463: 0.631709 0.834716 0.589077 0.709364 0.467876 0.521535 0.445105 0.223566 0.205436 0.144513 0.00525975  27.5866
#> outer mgc:  4217.137 
#>  53:    -96.912975: 0.623191 0.838384 0.591612 0.710755 0.468407 0.522122 0.450088 0.225337 0.202047 0.142101 0.00528500  27.6164
#> outer mgc:  3813.301 
#>  54:    -96.927619: 0.626130 0.839374 0.592800 0.710696 0.467798 0.521047 0.450428 0.226009 0.203536 0.141804 0.00528609  27.7159
#> outer mgc:  3275.102 
#>  55:    -96.941344: 0.633626 0.839508 0.592871 0.711675 0.468597 0.520734 0.452080 0.226002 0.204363 0.142919 0.00528373  27.9150
#> outer mgc:  5367.523 
#>  56:    -96.953941: 0.648499 0.839078 0.592276 0.711195 0.467637 0.520243 0.451059 0.225383 0.204036 0.142143 0.00528447  28.3133
#> outer mgc:  91.20114 
#>  57:    -96.965449: 0.663007 0.838436 0.591593 0.710283 0.467228 0.519854 0.450467 0.225472 0.203644 0.141673 0.00528054  28.6904
#> outer mgc:  169.5495 
#>  58:    -96.967491: 0.668964 0.838083 0.591585 0.710668 0.466347 0.520488 0.449882 0.224093 0.203429 0.141829 0.00528374  28.8833
#> outer mgc:  495.9119 
#>  59:    -96.968845: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  495.1999 
#>  60:    -96.968917: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  493.7759 
#>  61:    -96.969061: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  493.4911 
#>  62:    -96.969090: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  492.9215 
#>  63:    -96.969148: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.7823 
#>  64:    -96.969263: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.5545 
#>  65:    -96.969286: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.5089 
#>  66:    -96.969290: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.4178 
#>  67:    -96.969300: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.2355 
#>  68:    -96.969318: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1991 
#>  69:    -96.969322: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1918 
#>  70:    -96.969322: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1903 
#>  71:    -96.969323: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1874 
#>  72:    -96.969323: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1816 
#>  73:    -96.969323: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1804 
#>  74:    -96.969324: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1781 
#>  75:    -96.969324: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> outer mgc:  491.1776 
#>  76:    -96.969324: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#>  77:    -96.969324: 0.669333 0.838133 0.591261 0.710279 0.466760 0.520279 0.449768 0.224772 0.203167 0.141873 0.00528250  28.8811
#> Computing standard errors...
#> outer mgc:  491.1776 
#> outer mgc:  9023.392 
#> outer mgc:  8261.428 
#> outer mgc:  1308.121 
#> outer mgc:  346.914 
#> outer mgc:  1106.839 
#> outer mgc:  140.4563 
#> outer mgc:  1222.261 
#> outer mgc:  258.8762 
#> outer mgc:  1491.92 
#> outer mgc:  535.7422 
#> outer mgc:  1433.164 
#> outer mgc:  474.8577 
#> outer mgc:  1299.185 
#> outer mgc:  337.9714 
#> outer mgc:  1612.674 
#> outer mgc:  659.4646 
#> outer mgc:  1475.661 
#> outer mgc:  518.811 
#> outer mgc:  1063.454 
#> outer mgc:  95.80996 
#> outer mgc:  433814.8 
#> outer mgc:  1598167413 
#> outer mgc:  188.426 
#> outer mgc:  793.6266 
#> outer mgc:  1 
#> Warning: NaNs produced

# Example 2.3: Fast fitting without standard errors
# Useful for model exploration or large datasets
fit_fast <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  control = gkw_control(hessian = FALSE)
)
# Note: Cannot compute confint() without hessian
coef(fit_fast) # Point estimates still available
#> alpha:(Intercept)      alpha:batch1      alpha:batch2      alpha:batch3 
#>       0.669333319       0.838133049       0.591261201       0.710278918 
#>      alpha:batch4      alpha:batch5      alpha:batch6      alpha:batch7 
#>       0.466759877       0.520279363       0.449767828       0.224771574 
#>      alpha:batch8      alpha:batch9        alpha:temp  beta:(Intercept) 
#>       0.203167110       0.141873137       0.005282497      28.881137258 

# Example 2.4: Custom convergence tolerances
fit_tight <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  control = gkw_control(
    reltol = 1e-10, # Tighter convergence
    maxit = 2000 # More iterations allowed
  )
)
#> Warning: NaNs produced

# SECTION 3: Advanced Formula Specifications

# Example 3.1: Different predictors for different parameters
# alpha depends on batch, beta depends on temp
fit_diff <- gkwreg(
  yield ~ batch | temp,
  data = GasolineYield,
  family = "kw"
)
summary(fit_diff)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: kw 
#> 
#> Call:
#> gkwreg(formula = yield ~ batch | temp, data = GasolineYield, 
#>     family = "kw")
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.0989 -0.0233  0.0005 -0.0108  0.0118  0.0214 
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> alpha:(Intercept)  1.88013    0.12809  14.678  < 2e-16 ***
#> alpha:batch1       0.86260    0.05709  15.109  < 2e-16 ***
#> alpha:batch2       0.60776    0.05797  10.484  < 2e-16 ***
#> alpha:batch3       0.75706    0.05723  13.229  < 2e-16 ***
#> alpha:batch4       0.51423    0.05689   9.039  < 2e-16 ***
#> alpha:batch5       0.51897    0.06013   8.631  < 2e-16 ***
#> alpha:batch6       0.49736    0.05944   8.368  < 2e-16 ***
#> alpha:batch7       0.25282    0.05727   4.414 1.01e-05 ***
#> alpha:batch8       0.20432    0.06025   3.391 0.000695 ***
#> alpha:batch9       0.20744    0.06828   3.038 0.002381 ** 
#> beta:(Intercept)  51.66408    6.11692   8.446  < 2e-16 ***
#> beta:temp         -0.10073    0.01231  -8.181 2.82e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                        3%     98%
#> alpha:(Intercept)  1.6291  2.1312
#> alpha:batch1       0.7507  0.9745
#> alpha:batch2       0.4941  0.7214
#> alpha:batch3       0.6449  0.8692
#> alpha:batch4       0.4027  0.6257
#> alpha:batch5       0.4011  0.6368
#> alpha:batch6       0.3809  0.6139
#> alpha:batch7       0.1406  0.3651
#> alpha:batch8       0.0862  0.3224
#> alpha:batch9       0.0736  0.3413
#> beta:(Intercept)  39.6751 63.6530
#> beta:temp         -0.1249 -0.0766
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> 
#> Fitted parameter means:
#> alpha: 10.72
#> beta: 1.393e+12
#> gamma: 1
#> delta: 0
#> lambda: 1
#> 
#> Model fit statistics:
#> Number of observations: 32 
#> Number of parameters: 12 
#> Residual degrees of freedom: 20 
#> Log-likelihood: 80.5 
#> AIC: -137 
#> BIC: -119.4 
#> RMSE: 0.0345 
#> Efron's R2: 0.8931 
#> Mean Absolute Error: 0.02294 
#> 
#> Convergence status: Failed 
#> Iterations: 59 
#> 

# Example 3.2: Intercept-only for one parameter
# alpha varies with predictors, beta is constant
fit_partial <- gkwreg(
  yield ~ batch + temp | 1,
  data = GasolineYield,
  family = "kw"
)
#> Warning: NaNs produced

# Example 3.3: Complex model with interactions
fit_interact <- gkwreg(
  yield ~ batch * temp | temp + I(temp^2),
  data = GasolineYield,
  family = "kw"
)

# SECTION 4: Working with Different Families

# Example 4.1: Fit multiple families and compare
families <- c("beta", "kw", "ekw", "bkw", "gkw")
fits <- lapply(families, function(fam) {
  gkwreg(yield ~ batch + temp, data = GasolineYield, family = fam)
})
#> Warning: NaNs produced
#> Warning: NaNs produced
#> using C++ compiler: ‘g++ (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’
#> Warning: NaNs produced
names(fits) <- families

# Compare via information criteria
comparison <- data.frame(
  Family = families,
  LogLik = sapply(fits, logLik),
  AIC = sapply(fits, AIC),
  BIC = sapply(fits, BIC),
  npar = sapply(fits, function(x) x$npar)
)
print(comparison)
#>      Family   LogLik        AIC        BIC npar
#> beta   beta 45.26157  -66.52315  -48.93432   12
#> kw       kw 96.96932 -169.93865 -152.34982   12
#> ekw     ekw 97.31460 -168.62921 -149.57464   13
#> bkw     bkw 96.44294 -164.88587 -144.36557   14
#> gkw     gkw 96.49831 -162.99661 -141.01058   15

# Example 4.2: Formal nested model testing
fit_kw <- gkwreg(yield ~ batch + temp, GasolineYield, family = "kw")
#> Warning: NaNs produced
fit_ekw <- gkwreg(yield ~ batch + temp, GasolineYield, family = "ekw")
#> Warning: NaNs produced
fit_gkw <- gkwreg(yield ~ batch + temp, GasolineYield, family = "gkw")
anova(fit_kw, fit_ekw, fit_gkw)
#> Warning: negative deviance change detected; models may not be nested
#> Analysis of Deviance Table
#> 
#> Model 1: yield ~ batch + temp
#> Model 2: yield ~ batch + temp
#> Model 3: yield ~ batch + temp
#> 
#>         Resid. Df Resid. Dev Df Deviance Pr(>Chi)  
#> fit_kw   20.00000 -193.93865                       
#> fit_ekw  19.00000 -194.62921  1  0.69056  0.40597  
#> fit_gkw  17.00000 -192.99661  2 -1.63259           
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# SECTION 5: Link Functions and Scales

# Example 5.1: Custom link functions
fit_links <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  link = list(alpha = "sqrt", beta = "log")
)

# Example 5.2: Custom link scales
# Smaller scale = steeper response curve
fit_scale <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  link_scale = list(alpha = 5, beta = 15)
)
#> Warning: NaNs produced

# Example 5.3: Uniform link for all parameters
fit_uniform <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  link = "log" # Single string applied to all
)
#> Warning: NaNs produced

# SECTION 6: Prediction and Inference

# Fit model for prediction examples
fit <- gkwreg(yield ~ batch + temp, GasolineYield, family = "kw")
#> Warning: NaNs produced

# Example 6.1: Confidence intervals at different levels
confint(fit, level = 0.95) # 95% CI
#> Warning: some standard errors are NA or infinite; intervals may be unreliable
#>                         2.5 %     97.5 %
#> alpha:(Intercept)  0.61309049  0.7255762
#> alpha:batch1       0.78581980  0.8904463
#> alpha:batch2       0.53531608  0.6472063
#> alpha:batch3       0.65446611  0.7660917
#> alpha:batch4       0.41447097  0.5190488
#> alpha:batch5       0.46459924  0.5759595
#> alpha:batch6       0.39388604  0.5056496
#> alpha:batch7       0.17258723  0.2769559
#> alpha:batch8       0.14773407  0.2586001
#> alpha:batch9       0.07935147  0.2043948
#> alpha:temp                NaN        NaN
#> beta:(Intercept)  28.03819235 29.7240822
confint(fit, level = 0.90) # 90% CI
#> Warning: some standard errors are NA or infinite; intervals may be unreliable
#>                          5 %       95 %
#> alpha:(Intercept)  0.6221328  0.7165338
#> alpha:batch1       0.7942304  0.8820357
#> alpha:batch2       0.5443106  0.6382118
#> alpha:batch3       0.6634393  0.7571185
#> alpha:batch4       0.4228776  0.5106421
#> alpha:batch5       0.4735511  0.5670076
#> alpha:batch6       0.4028704  0.4966653
#> alpha:batch7       0.1809771  0.2685661
#> alpha:batch8       0.1566462  0.2496880
#> alpha:batch9       0.0894033  0.1943430
#> alpha:temp               NaN        NaN
#> beta:(Intercept)  28.1737156 29.5885589
confint(fit, level = 0.99) # 99% CI
#> Warning: some standard errors are NA or infinite; intervals may be unreliable
#>                         0.5 %     99.5 %
#> alpha:(Intercept)  0.59541771  0.7432489
#> alpha:batch1       0.76938179  0.9068843
#> alpha:batch2       0.51773685  0.6647856
#> alpha:batch3       0.63692846  0.7836294
#> alpha:batch4       0.39804060  0.5354792
#> alpha:batch5       0.44710328  0.5934554
#> alpha:batch6       0.37632671  0.5232089
#> alpha:batch7       0.15618972  0.2933534
#> alpha:batch8       0.13031575  0.2760185
#> alpha:batch9       0.05970574  0.2240405
#> alpha:temp                NaN        NaN
#> beta:(Intercept)  27.77331987 29.9889546

# SECTION 7: Diagnostic Plots and Model Checking

fit <- gkwreg(yield ~ batch + temp, GasolineYield, family = "kw")
#> Warning: NaNs produced

# Example 7.1: All diagnostic plots (default)
par(mfrow = c(3, 2))
plot(fit, ask = FALSE)
#> Simulating envelope ( 100 iterations): .......... Done!


# Example 7.2: Select specific plots
par(mfrow = c(3, 1))
plot(fit, which = c(2, 4, 5)) # Cook's distance, Residuals, Half-normal
#> Simulating envelope ( 100 iterations): .......... Done!


# Example 7.3: Using ggplot2 for modern graphics
plot(fit, use_ggplot = TRUE, arrange_plots = TRUE)
#> Simulating envelope ( 100 iterations): .......... Done!
#> Warning: Removed 1 row containing missing values or values outside the scale range
#> (`geom_segment()`).


# Example 7.4: Customized half-normal plot
par(mfrow = c(1, 1))
plot(fit,
  which = 5,
  type = "quantile",
  nsim = 200, # More simulations for smoother envelope
  level = 0.95
) # 95% confidence envelope
#> Simulating envelope ( 200 iterations): .......... Done!


# Example 7.5: Extract diagnostic data programmatically
diagnostics <- plot(fit, save_diagnostics = TRUE)
#> Simulating envelope ( 100 iterations): .......... Done!
head(diagnostics$data) # Residuals, Cook's distance, etc.
#>   index y_obs    fitted    resid abs_resid  cook_dist  leverage  linpred
#> 1     1 0.122 0.1110263 1.872237  1.872237 0.08026648 0.3755669 2.590378
#> 2     2 0.223 0.2173790 1.872237  1.872237 0.08500820 0.3853667 2.960153
#> 3     3 0.347 0.3528410 1.872237  1.872237 0.09289227 0.4005540 3.329928
#> 4     4 0.457 0.4674384 1.872237  1.872237 0.08854416 0.3923400 3.657443
#> 5     5 0.080 0.0716840 1.872237  1.872237 0.08716616 0.3896549 2.412179
#> 6     6 0.131 0.1403505 1.872237  1.872237 0.08129922 0.3777472 2.702716

# SECTION 8: Real Data Example - Food Expenditure

# Load and prepare data
data(FoodExpenditure, package = "betareg")
food_data <- FoodExpenditure
food_data$prop <- food_data$food / food_data$income

# Example 8.1: Basic model
fit_food <- gkwreg(
  prop ~ persons | income,
  data = food_data,
  family = "kw"
)
summary(fit_food)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: kw 
#> 
#> Call:
#> gkwreg(formula = prop ~ persons | income, data = food_data, family = "kw")
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.1668 -0.0417  0.0098 -0.0047  0.0396  0.1527 
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> alpha:(Intercept)  1.26876    0.14206   8.931  < 2e-16 ***
#> alpha:persons      0.07210    0.01895   3.805 0.000142 ***
#> beta:(Intercept)   3.21312    0.63879   5.030  4.9e-07 ***
#> beta:income        0.03623    0.00922   3.930  8.5e-05 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                       3%    98%
#> alpha:(Intercept) 0.9903 1.5472
#> alpha:persons     0.0350 0.1092
#> beta:(Intercept)  1.9611 4.4651
#> beta:income       0.0182 0.0543
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> 
#> Fitted parameter means:
#> alpha: 4.638
#> beta: 244.4
#> gamma: 1
#> delta: 0
#> lambda: 1
#> 
#> Model fit statistics:
#> Number of observations: 38 
#> Number of parameters: 4 
#> Residual degrees of freedom: 34 
#> Log-likelihood: 46.34 
#> AIC: -84.69 
#> BIC: -78.14 
#> RMSE: 0.07442 
#> Efron's R2: 0.4465 
#> Mean Absolute Error: 0.05784 
#> 
#> Convergence status: Successful 
#> Iterations: 18 
#> 

# Example 8.2: Compare with Beta regression
fit_food_beta <- gkwreg(
  prop ~ persons | income,
  data = food_data,
  family = "beta"
)

# Which fits better?
AIC(fit_food, fit_food_beta)
#>               df       AIC
#> fit_food       4 -84.68830
#> fit_food_beta  4 -70.28298

# Example 8.3: Model diagnostics
par(mfrow = c(3, 1))
plot(fit_food, which = c(2, 5, 6))
#> Simulating envelope ( 100 iterations): .......... Done!


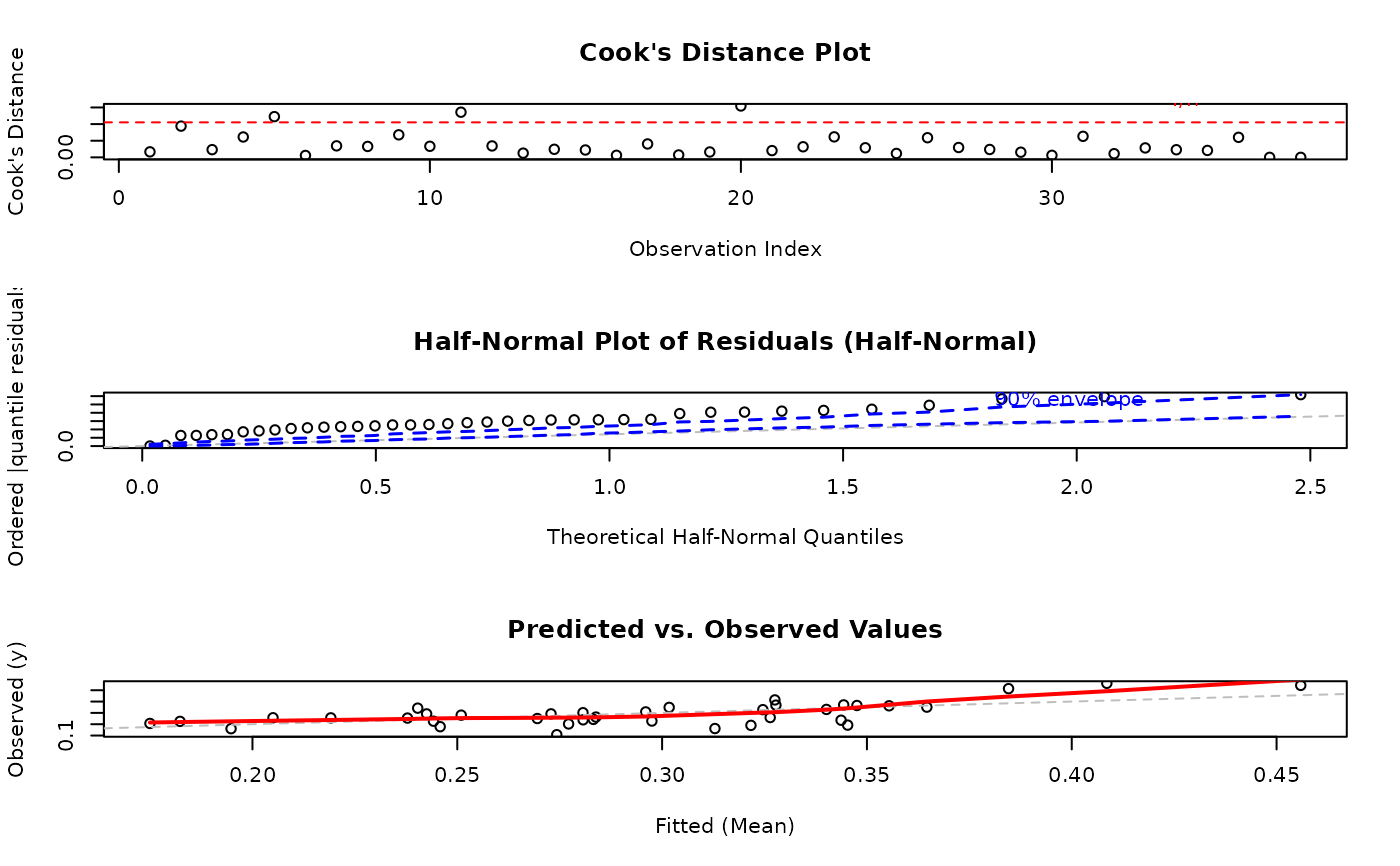# Example 8.4: Interpretation via effects
# How does proportion spent on food change with income?
income_seq <- seq(min(food_data$income), max(food_data$income), length = 50)
pred_data <- data.frame(
  persons = median(food_data$persons),
  income = income_seq
)
pred_food <- predict(fit_food, newdata = pred_data, type = "response")

par(mfrow = c(1, 1))
plot(food_data$income, food_data$prop,
  xlab = "Income", ylab = "Proportion Spent on Food",
  main = "Food Expenditure Pattern"
)
lines(income_seq, pred_food, col = "red", lwd = 2)


# SECTION 9: Simulation Studies

# Example 9.1: Simple Kumaraswamy simulation
set.seed(123)
n <- 500
x1 <- runif(n, -2, 2)
x2 <- rnorm(n)

# True model: log(alpha) = 0.8 + 0.3*x1, log(beta) = 1.2 - 0.2*x2
eta_alpha <- 0.8 + 0.3 * x1
eta_beta <- 1.2 - 0.2 * x2
alpha_true <- exp(eta_alpha)
beta_true <- exp(eta_beta)

# Generate response
y <- rkw(n, alpha = alpha_true, beta = beta_true)
sim_data <- data.frame(y = y, x1 = x1, x2 = x2)

# Fit and check parameter recovery
fit_sim <- gkwreg(y ~ x1 | x2, data = sim_data, family = "kw")

# Compare estimated vs true coefficients
cbind(
  True = c(0.8, 0.3, 1.2, -0.2),
  Estimated = coef(fit_sim),
  SE = fit_sim$se
)
#>                   True  Estimated         SE
#> alpha:(Intercept)  0.8  0.8013394 0.04562729
#> alpha:x1           0.3  0.3011747 0.02418262
#> beta:(Intercept)   1.2  1.1896310 0.07482055
#> beta:x2           -0.2 -0.2419618 0.04607844

# Example 9.2: Complex simulation with all five parameters
set.seed(2203)
n <- 2000
x <- runif(n, -1, 1)

# True parameters
alpha <- exp(0.5 + 0.3 * x)
beta <- exp(1.0 - 0.2 * x)
gamma <- exp(0.7 + 0.4 * x)
delta <- plogis(0.0 + 0.5 * x) # logit scale
lambda <- exp(-0.3 + 0.2 * x)

# Generate from GKw
y <- rgkw(n,
  alpha = alpha, beta = beta, gamma = gamma,
  delta = delta, lambda = lambda
)
sim_data2 <- data.frame(y = y, x = x)

# Fit GKw model
fit_gkw <- gkwreg(
  y ~ x | x | x | x | x,
  data = sim_data2,
  family = "gkw",
  control = gkw_control(method = "L-BFGS-B", maxit = 2000)
)
#> Warning: NaNs produced
summary(fit_gkw)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: gkw 
#> 
#> Call:
#> gkwreg(formula = y ~ x | x | x | x | x, data = sim_data2, family = "gkw", 
#>     control = gkw_control(method = "L-BFGS-B", maxit = 2000))
#> 
#> Residuals:
#>     Min  Q1.25%  Median    Mean  Q3.75%     Max 
#> -0.3455 -0.0929  0.0205  0.0337  0.1502  0.6360 
#> 
#> Coefficients:
#>                    Estimate Std. Error z value Pr(>|z|)    
#> alpha:(Intercept)   0.97085    0.61249   1.585   0.1129    
#> alpha:x             0.75943    1.04259   0.728   0.4664    
#> beta:(Intercept)   -0.43418    0.08793  -4.938  7.9e-07 ***
#> beta:x             -0.42851    0.52143  -0.822   0.4112    
#> gamma:(Intercept)   1.12970        NaN     NaN      NaN    
#> gamma:x             1.16488    0.47263   2.465   0.0137 *  
#> delta:(Intercept)  -0.19516        NaN     NaN      NaN    
#> delta:x             0.61546    1.08639   0.567   0.5710    
#> lambda:(Intercept) -1.00510    0.44824  -2.242   0.0249 *  
#> lambda:x           -0.83449    1.49367  -0.559   0.5764    
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                         3%     98%
#> alpha:(Intercept)  -0.2296  2.1713
#> alpha:x            -1.2840  2.8029
#> beta:(Intercept)   -0.6065 -0.2618
#> beta:x             -1.4505  0.5935
#> gamma:(Intercept)      NaN     NaN
#> gamma:x             0.2385  2.0912
#> delta:(Intercept)      NaN     NaN
#> delta:x            -1.5138  2.7447
#> lambda:(Intercept) -1.8836 -0.1266
#> lambda:x           -3.7620  2.0930
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> gamma: log
#> delta: logit
#> lambda: log
#> 
#> Fitted parameter means:
#> alpha: 2.873
#> beta: 0.6702
#> gamma: 3.782
#> delta: 4.513
#> lambda: 0.4125
#> 
#> Model fit statistics:
#> Number of observations: 2000 
#> Number of parameters: 10 
#> Residual degrees of freedom: 1990 
#> Log-likelihood: 860.9 
#> AIC: -1702 
#> BIC: -1646 
#> RMSE: 0.1708 
#> Efron's R2: 0.3325 
#> Mean Absolute Error: 0.1374 
#> 
#> Convergence status: Failed 
#> Iterations: 116 
#> 

# SECTION 10: Handling Convergence Issues

# Example 10.1: Try different optimizers
methods <- c("nlminb", "BFGS", "Nelder-Mead", "CG")
fits_methods <- lapply(methods, function(m) {
  tryCatch(
    gkwreg(yield ~ batch + temp, GasolineYield,
      family = "kw",
      control = gkw_control(method = m, silent = TRUE)
    ),
    error = function(e) NULL
  )
})
#> Warning: NaNs produced
#> Warning: NaNs produced
names(fits_methods) <- methods

# Check which converged
converged <- sapply(fits_methods, function(f) {
  if (is.null(f)) {
    return(FALSE)
  }
  f$convergence
})
print(converged)
#>      nlminb        BFGS Nelder-Mead          CG 
#>       FALSE        TRUE        TRUE       FALSE 

# Example 10.2: Verbose mode for debugging
fit_debug <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  control = gkw_control(
    method = "BFGS",
    silent = TRUE,
    trace = 0, # 2, Maximum verbosity
    maxit = 1000
  )
)

# SECTION 11: Memory and Performance Optimization

# Example 11.1: Minimal object for large datasets
fit_minimal <- gkwreg(
  yield ~ batch + temp,
  data = GasolineYield,
  family = "kw",
  model = FALSE, # Don't store model frame
  x = FALSE, # Don't store design matrices
  y = FALSE, # Don't store response
  control = gkw_control(hessian = FALSE) # Skip Hessian
)

# Much smaller object
object.size(fit_minimal)
#> 745256 bytes

# Trade-off: Limited post-fitting capabilities
# Can still use: coef(), logLik(), AIC(), BIC()
# Cannot use: predict(), some diagnostics

# Example 11.2: Fast exploratory analysis
# Fit many models quickly without standard errors
formulas <- list(
  yield ~ batch,
  yield ~ temp,
  yield ~ batch + temp,
  yield ~ batch * temp
)

fast_fits <- lapply(formulas, function(f) {
  gkwreg(f, GasolineYield,
    family = "kw",
    control = gkw_control(hessian = FALSE),
    model = FALSE, x = FALSE, y = FALSE
  )
})

# Compare models via AIC
sapply(fast_fits, AIC)
#> [1]  -42.93436  -74.90259 -169.93865 -292.55289

# Refit best model with full inference
best_formula <- formulas[[which.min(sapply(fast_fits, AIC))]]
fit_final <- gkwreg(best_formula, GasolineYield, family = "kw")
#> Warning: NaNs produced
summary(fit_final)
#> 
#> Generalized Kumaraswamy Regression Model Summary
#> 
#> Family: kw 
#> 
#> Call:
#> gkwreg(formula = best_formula, data = GasolineYield, family = "kw")
#> 
#> Residuals:
#>           Min        Q1.25%        Median          Mean        Q3.75% 
#> -1.030369e+22 -1.030369e+22 -1.030369e+22 -1.030369e+22 -1.030369e+22 
#>           Max 
#> -1.030369e+22 
#> 
#> Coefficients:
#>                     Estimate Std. Error  z value Pr(>|z|)    
#> alpha:(Intercept)  2.101e+00  4.024e-03    522.2   <2e-16 ***
#> alpha:batch1       1.255e-01        NaN      NaN      NaN    
#> alpha:batch2      -2.415e-01  9.235e-04   -261.5   <2e-16 ***
#> alpha:batch3      -3.067e-01  1.713e-03   -179.1   <2e-16 ***
#> alpha:batch4      -3.853e-01  3.984e-05  -9670.6   <2e-16 ***
#> alpha:batch5      -7.100e-01        NaN      NaN      NaN    
#> alpha:batch6      -2.994e-01  7.516e-05  -3983.1   <2e-16 ***
#> alpha:batch7      -6.844e-01  1.121e-04  -6104.4   <2e-16 ***
#> alpha:batch8      -9.483e-01  1.895e-04  -5004.7   <2e-16 ***
#> alpha:batch9      -3.894e-01  1.951e-05 -19954.5   <2e-16 ***
#> alpha:temp         2.980e-03        NaN      NaN      NaN    
#> alpha:batch1:temp  1.697e-03        NaN      NaN      NaN    
#> alpha:batch2:temp  2.170e-03        NaN      NaN      NaN    
#> alpha:batch3:temp  2.813e-03        NaN      NaN      NaN    
#> alpha:batch4:temp  2.174e-03        NaN      NaN      NaN    
#> alpha:batch5:temp  3.178e-03        NaN      NaN      NaN    
#> alpha:batch6:temp  1.894e-03        NaN      NaN      NaN    
#> alpha:batch7:temp  2.360e-03        NaN      NaN      NaN    
#> alpha:batch8:temp  3.080e-03        NaN      NaN      NaN    
#> alpha:batch9:temp  1.325e-03        NaN      NaN      NaN    
#> beta:(Intercept)   5.069e+01  1.326e-01    382.2   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Confidence intervals (95%):
#>                        3%     98%
#> alpha:(Intercept)  2.0934  2.1091
#> alpha:batch1          NaN     NaN
#> alpha:batch2      -0.2433 -0.2397
#> alpha:batch3      -0.3100 -0.3033
#> alpha:batch4      -0.3854 -0.3852
#> alpha:batch5          NaN     NaN
#> alpha:batch6      -0.2995 -0.2992
#> alpha:batch7      -0.6846 -0.6842
#> alpha:batch8      -0.9486 -0.9479
#> alpha:batch9      -0.3894 -0.3893
#> alpha:temp            NaN     NaN
#> alpha:batch1:temp     NaN     NaN
#> alpha:batch2:temp     NaN     NaN
#> alpha:batch3:temp     NaN     NaN
#> alpha:batch4:temp     NaN     NaN
#> alpha:batch5:temp     NaN     NaN
#> alpha:batch6:temp     NaN     NaN
#> alpha:batch7:temp     NaN     NaN
#> alpha:batch8:temp     NaN     NaN
#> alpha:batch9:temp     NaN     NaN
#> beta:(Intercept)  50.4279 50.9477
#> 
#> Link functions:
#> alpha: log
#> beta: log
#> 
#> Fitted parameter means:
#> alpha: 31.63
#> beta: 1.03e+22
#> gamma: 1
#> delta: 0
#> lambda: 1
#> 
#> Model fit statistics:
#> Number of observations: 32 
#> Number of parameters: 21 
#> Residual degrees of freedom: 11 
#> Log-likelihood: 167.3 
#> AIC: -292.6 
#> BIC: -261.8 
#> RMSE: 1.03e+22 
#> Efron's R2: -9.532e+45 
#> Mean Absolute Error: 1.03e+22 
#> 
#> Convergence status: Failed 
#> Iterations: 286 
#> 

# SECTION 12: Model Selection and Comparison

# Example 12.1: Nested model testing
fit1 <- gkwreg(yield ~ 1, GasolineYield, family = "kw")
fit2 <- gkwreg(yield ~ batch, GasolineYield, family = "kw")
fit3 <- gkwreg(yield ~ batch + temp, GasolineYield, family = "kw")
#> Warning: NaNs produced

# Likelihood ratio tests
anova(fit1, fit2, fit3)
#> Analysis of Deviance Table
#> 
#> Model 1: yield ~ 1
#> Model 2: yield ~ batch
#> Model 3: yield ~ batch + temp
#> 
#>      Resid. Df Resid. Dev Df  Deviance Pr(>Chi)    
#> fit1  30.00000  -57.02258                          
#> fit2  21.00000  -64.93436  9   7.91178  0.54306    
#> fit3  20.00000 -193.93865  1 129.00429  < 1e-04 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Example 12.2: Information criteria table
models <- list(
  "Intercept only" = fit1,
  "Batch effect" = fit2,
  "Batch + Temp" = fit3
)

ic_table <- data.frame(
  Model = names(models),
  df = sapply(models, function(m) m$npar),
  LogLik = sapply(models, logLik),
  AIC = sapply(models, AIC),
  BIC = sapply(models, BIC),
  Delta_AIC = sapply(models, AIC) - min(sapply(models, AIC))
)
print(ic_table)
#>                         Model df   LogLik        AIC        BIC Delta_AIC
#> Intercept only Intercept only  2 28.51129  -53.02258  -50.09111  116.9161
#> Batch effect     Batch effect 11 32.46718  -42.93436  -26.81126  127.0043
#> Batch + Temp     Batch + Temp 12 96.96932 -169.93865 -152.34982    0.0000

# Example 12.3: Cross-validation for predictive performance
# 5-fold cross-validation
set.seed(2203)
n <- nrow(GasolineYield)
folds <- sample(rep(1:5, length.out = n))

cv_rmse <- sapply(1:5, function(fold) {
  train <- GasolineYield[folds != fold, ]
  test <- GasolineYield[folds == fold, ]

  fit_train <- gkwreg(yield ~ batch + temp, train,
    family = "kw"
  )
  pred_test <- predict(fit_train, newdata = test, type = "response")

  sqrt(mean((test$yield - pred_test)^2))
})
#> Warning: NaNs produced
#> Warning: NaNs produced
#> Warning: NaNs produced
#> Warning: NaNs produced

cat("Cross-validated RMSE:", mean(cv_rmse), "\n")
#> Cross-validated RMSE: 0.09025705 
# }