Density of the Generalized Kumaraswamy Distribution

Computes the probability density function (PDF) for the five-parameter Generalized Kumaraswamy (GKw) distribution, defined on the interval (0, 1).

Usage

dgkw(x, alpha, beta, gamma, delta, lambda, log_prob = FALSE)

Arguments

x: Vector of quantiles (values between 0 and 1).
alpha: Shape parameter alpha > 0. Can be a scalar or a vector. Default: 1.0.
beta: Shape parameter beta > 0. Can be a scalar or a vector. Default: 1.0.
gamma: Shape parameter gamma > 0. Can be a scalar or a vector. Default: 1.0.
delta: Shape parameter delta >= 0. Can be a scalar or a vector. Default: 0.0.
lambda: Shape parameter lambda > 0. Can be a scalar or a vector. Default: 1.0.
log_prob: Logical; if TRUE, the logarithm of the density is returned. Default: FALSE.

Value

A vector of density values ($f(x)$) or log-density values ($\log(f(x))$). The length of the result is determined by the recycling rule applied to the arguments (x, alpha, beta, gamma, delta, lambda). Returns 0 (or -Inf if log_prob = TRUE) for x outside the interval (0, 1), or NaN if parameters are invalid.

Details

The probability density function of the Generalized Kumaraswamy (GKw) distribution with parameters alpha ($\alpha$), beta ($\beta$), gamma ($\gamma$), delta ($\delta$), and lambda ($\lambda$) is given by: $$ f(x; \alpha, \beta, \gamma, \delta, \lambda) = \frac{\lambda \alpha \beta x^{\alpha-1}(1-x^{\alpha})^{\beta-1}} {B(\gamma, \delta+1)} [1-(1-x^{\alpha})^{\beta}]^{\gamma\lambda-1} [1-[1-(1-x^{\alpha})^{\beta}]^{\lambda}]^{\delta} $$ for $x \in (0,1)$, where $B(a, b)$ is the Beta function beta.

This distribution was proposed by Cordeiro & de Castro (2011) and includes several other distributions as special cases:

Kumaraswamy (Kw): gamma = 1, delta = 0, lambda = 1
Exponentiated Kumaraswamy (EKw): gamma = 1, delta = 0
Beta-Kumaraswamy (BKw): lambda = 1
Generalized Beta type 1 (GB1 - implies McDonald): alpha = 1, beta = 1
Beta distribution: alpha = 1, beta = 1, lambda = 1

The function includes checks for valid parameters and input values x. It uses numerical stabilization for x close to 0 or 1.

References

Cordeiro, G. M., & de Castro, M. (2011). A new family of generalized distributions. Journal of Statistical Computation and Simulation, 81(7), 883-898.

Kumaraswamy, P. (1980). A generalized probability density function for double-bounded random processes. Journal of Hydrology, 46(1-2), 79-88.

Author

Lopes, J. E.

Examples

# \donttest{
# Simple density evaluation at a point
dgkw(0.5, alpha = 2, beta = 3, gamma = 1, delta = 0, lambda = 1) # Kw case
#> [1] 1.6875

# Plot the PDF for various parameter sets
x_vals <- seq(0.01, 0.99, by = 0.01)

# Standard Kumaraswamy (gamma=1, delta=0, lambda=1)
pdf_kw <- dgkw(x_vals, alpha = 2, beta = 3, gamma = 1, delta = 0, lambda = 1)

# Beta equivalent (alpha=1, beta=1, lambda=1) - Beta(gamma, delta+1)
pdf_beta <- dgkw(x_vals, alpha = 1, beta = 1, gamma = 2, delta = 3, lambda = 1)
# Compare with stats::dbeta
pdf_beta_check <- stats::dbeta(x_vals, shape1 = 2, shape2 = 3 + 1)
# max(abs(pdf_beta - pdf_beta_check)) # Should be close to zero

# Exponentiated Kumaraswamy (gamma=1, delta=0)
pdf_ekw <- dgkw(x_vals, alpha = 2, beta = 3, gamma = 1, delta = 0, lambda = 2)

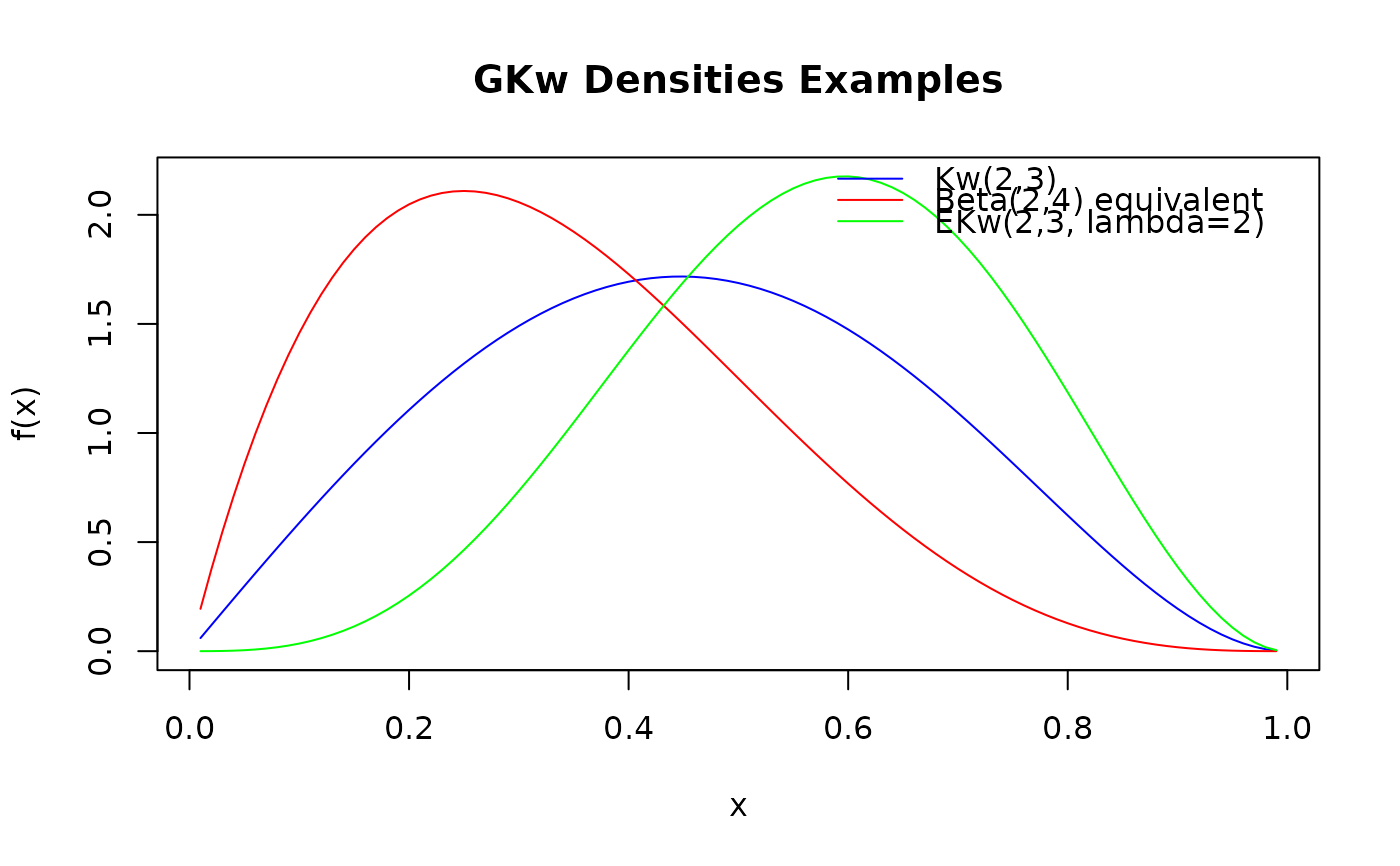
plot(x_vals, pdf_kw, type = "l", ylim = range(c(pdf_kw, pdf_beta, pdf_ekw)),
     main = "GKw Densities Examples", ylab = "f(x)", xlab="x", col = "blue")
lines(x_vals, pdf_beta, col = "red")
lines(x_vals, pdf_ekw, col = "green")
legend("topright", legend = c("Kw(2,3)", "Beta(2,4) equivalent", "EKw(2,3, lambda=2)"),
       col = c("blue", "red", "green"), lty = 1, bty = "n")


# Log-density
log_pdf_val <- dgkw(0.5, 2, 3, 1, 0, 1, log_prob = TRUE)
print(log_pdf_val)
#> [1] 0.5232481
print(log(dgkw(0.5, 2, 3, 1, 0, 1))) # Should match
#> [1] 0.5232481

# }