Capítulo - 2 Estatística descritiva
Técnicas para descrever e sumarizar conjuntos de dados de natureza diversa fazem parte da estatística descritiva. Entre estas técnicas, estão tabelas de frequências, resumos numéricos e gráficos de acordo com o tipo de variável envolvida. Neste capítulo trataremos destas técnicas sempre com foco em conjuntos de dados do Censo de Educação Superior do INEP.
2.1 Variáveis categóricas
No ramo esquerdo da figura 1.7 temos as variáveis qualitativas. Elas são em geral, variáveis em formato de texto ou números inteiros que representam atributos nominais ou ordinais de determinada observação ou indivíduo de uma base de dados. A seguir vamos apresentar algumas técnicas descritivas para este tipo de variável e para melhor exemplificar vamos trabalhar com mais algumas variáveis do conjunto de dados dos docentes do ensino superior do censo do INEP de 2017. Para mais informações sobre as variáveis consulte o dicionário de dados da base. As melhores técnicas utilizadas são variáveis categóricas são contagens/frequências, proporções/percentuais e gráficos.
# Classes dos dados
base_docentes <- rnp::dm_docente
# Variáveis importantes da base de Docentes
vars_doc <- c("CO_IES", "DESC_TP_CATEGORIA_ADMINISTRATIVA", "DESC_TP_SEXO",
"NU_IDADE", "DESC_TP_ESCOLARIDADE","DESC_TP_REGIME_TRABALHO",
"CO_DOCENTE","DESC_TP_SITUACAO")
base_docentes <- base_docentes %>%
dplyr::mutate(faixaIdade = if_else(NU_IDADE <= 30, "01.Até 30 anos",
if_else(NU_IDADE <= 40, "02.Entre 30 e 40 anos",
if_else(NU_IDADE <= 50, "03.Entre 40 e 50 anos",
if_else(NU_IDADE <= 60, "04.Entre 50 e 60 anos",
"05.Acima de 60 anos"))))) %>%
dplyr::rename(cdDocente = CO_DOCENTE,
cdIES = CO_IES,
catAdm = DESC_TP_CATEGORIA_ADMINISTRATIVA,
situacao = DESC_TP_SITUACAO,
escolaridade = DESC_TP_ESCOLARIDADE,
faixaIdade = faixaIdade,
regimeTrabalho = DESC_TP_REGIME_TRABALHO,
sexo = DESC_TP_SEXO,
idade = NU_IDADE) %>%
dplyr::arrange(faixaIdade)
rnp::rnp_atributos(base_docentes) %>%
knitr::kable(booktabs = TRUE, format = tb_formata,
caption = "Atributos da base dos docentes") %>%
kableExtra::kable_styling(latex_options = "hold_position")| classeBase | comprimento | variaveis | classeVars |
|---|---|---|---|
| data.frame | 392036 linhas e 42 colunas | NU_ANO_CENSO | integer |
| data.frame | 392036 linhas e 42 colunas | cdIES | integer |
| data.frame | 392036 linhas e 42 colunas | CO_DOCENTE_IES | integer |
| data.frame | 392036 linhas e 42 colunas | cdDocente | numeric |
| data.frame | 392036 linhas e 42 colunas | NU_ANO_NASCIMENTO | integer |
| data.frame | 392036 linhas e 42 colunas | NU_MES_NASCIMENTO | integer |
| data.frame | 392036 linhas e 42 colunas | NU_DIA_NASCIMENTO | integer |
| data.frame | 392036 linhas e 42 colunas | idade | integer |
| data.frame | 392036 linhas e 42 colunas | CO_PAIS_ORIGEM | integer |
| data.frame | 392036 linhas e 42 colunas | CO_UF_NASCIMENTO | integer |
| data.frame | 392036 linhas e 42 colunas | CO_MUNICIPIO_NASCIMENTO | integer |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_EAD | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_EXTENSAO | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_GESTAO | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_GRAD_PRESENCIAL | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_PESQUISA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_POS_EAD | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_POS_PRESENCIAL | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_ATUACAO_SEQUENCIAL | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_BOLSA_PESQUISA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_AUDITIVA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_BAIXA_VISAO | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_CEGUEIRA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_FISICA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_INTELECTUAL | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_MULTIPLA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_SURDEZ | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_DEFICIENCIA_SURDOCEGUEIRA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_EXERCICIO_DATA_REFERENCIA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_SUBSTITUTO | character |
| data.frame | 392036 linhas e 42 colunas | DESC_IN_VISITANTE | character |
| data.frame | 392036 linhas e 42 colunas | catAdm | character |
| data.frame | 392036 linhas e 42 colunas | DESC_TP_COR_RACA | character |
| data.frame | 392036 linhas e 42 colunas | DESC_TP_DEFICIENCIA | character |
| data.frame | 392036 linhas e 42 colunas | escolaridade | character |
| data.frame | 392036 linhas e 42 colunas | DESC_TP_NACIONALIDADE | character |
| data.frame | 392036 linhas e 42 colunas | DESC_TP_ORGANIZACAO_ACADEMICA | character |
| data.frame | 392036 linhas e 42 colunas | regimeTrabalho | character |
| data.frame | 392036 linhas e 42 colunas | sexo | character |
| data.frame | 392036 linhas e 42 colunas | situacao | character |
| data.frame | 392036 linhas e 42 colunas | DESC_TP_VISITANTE_IFES_VINCULO | character |
| data.frame | 392036 linhas e 42 colunas | faixaIdade | character |
A tabela 2.1 mostra uma parte dos dados dos decentes contendo algumas variáveis que exploraremos mais adiante. Temos 392036 observações ou docentes de ensino superior no censo de 2017.
2.1.1 Tabelas de frequências
As tabelas de frequência são muito úteis para analisar a distribuição dos dados de uma variável segundo suas categorias ou classes, com elas podemos analisar contagens e proporções de cada categoria da variável. Para isso, entra em cena os seguintes conceitos:
- Classe: É a descrição da categoria ou nível da variável;
- Frequência absoluta: trata-se da contagem de observações pertencentes a uma dada categoria da variável;
- Frequência relativa: trata-se da contagem de observações pertencentes a uma dada categoria da variável dividida pelo total de observações. É a representação percentual da frequência absoluta;
- Frequência absoluta acumulada: é dada pelo soma acumulada das frequências absolutas;
- Frequência relativa acumulada: é dada pelo soma acumulada das frequências relativas;
A junção destas estatísticas constitui uma tabela de frequências que podem ser simples ou de dupla entrada, também chamada de tabela de contingência:
2.1.1.1 Tabela de frequências simples
São tabelas simples para apenas uma variável. No pacote rnp inserimos a função rnp_freq() para realizar a tabulação dos dados.
rnp::rnp_freq(x = base_docentes$escolaridade,
sortd = FALSE, digits = 3) %>%
knitr::kable(booktabs = TRUE, format = tb_formata,
caption = "Frequências simples escolaridade do docente") %>%
kableExtra::kable_styling(latex_options = "hold_position")| classe | fa | fr | Faa | Fra |
|---|---|---|---|---|
| 1. Sem graduação | 10 | 0.000 | 10 | 0.000 |
| 2. Graduação | 4613 | 0.012 | 4623 | 0.012 |
| 3. Especialização | 72301 | 0.184 | 76924 | 0.196 |
| 4. Mestrado | 154285 | 0.394 | 231209 | 0.590 |
| 5. Doutorado | 160827 | 0.410 | 392036 | 1.000 |
A tabela 2.2 exemplifica uma tabela de frequência simples onde podemos analisar diretamente os dados da variável escolaridade dos docentes. Podemos ver que há 392.036 docentes e que destes, 39,4% possuem mestrado e 41,0% doutorado. Juntas, estas duas categorias representam 80,0% da base. Se somarmos os especialistas, temos um total de 98,8%.
2.1.1.2 Tabela de frequências de dupla entrada
Quando desejamos analisar a relação entre duas variáveis categóricas, podemos aplicar a mesma ideia da tabela de frequências simples, porém combinando as variáveis de forma cruzada. Sejam \(X\) e \(Y\) duas variáveis categóricas quaisquer, então podemos construir tabelas cruzadas dos tipos \(2 \times 2; 2 \times l; k \times 2;k \times l\) onde \(k\) e \(l\) são respetivamente o total de classes da variável \(X\) e total de classes da variável \(Y\). Caso uma variável possua apenas uma classe \(1 \times l; k \times 1\)em geral não faz sentido analisar tabela cruzada.
Mais adiante falaremos de medidas de associação entre duas variáveis categóricas e para antecipar a leitura deste tipo de dado, apresentamos a tabela 2.1 que ilustra a forma genérica de uma tabela de dupla entrada. Para simplificar a notação, trataremos o caso das frequências absolutas e assumimos que cada cruzamento de \(X\) com \(x_1,x_2,x_3,...,x_k\) classes por \(Y\) com \(y_1,y_2,y_3,...,y_l\) classes dado pelo par \((x_i;y_j)\) seja representado por \(n_{ij}\) com \(i=1,2,3,...,k\) e \(j=1,2,3,...,l\).
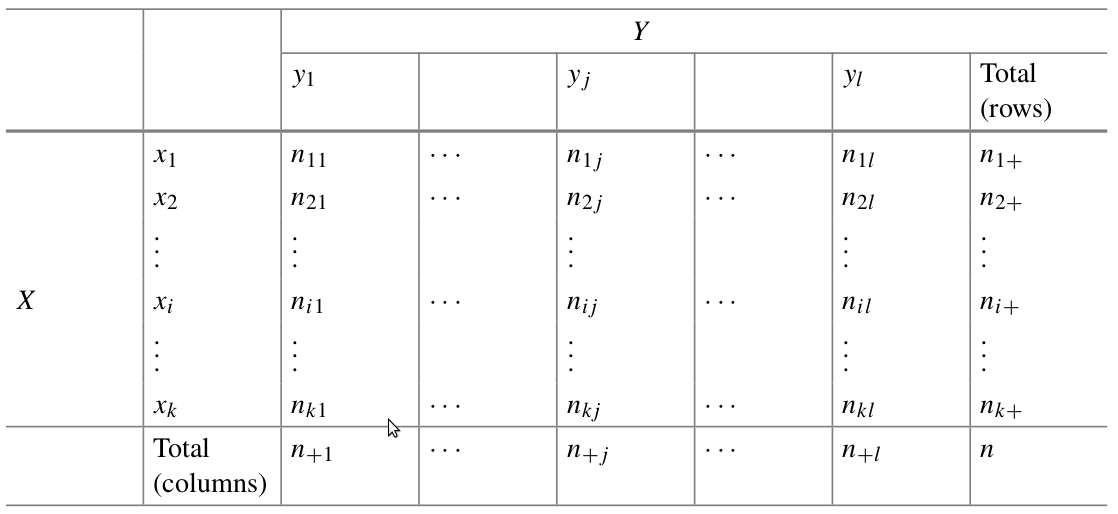
Figura 2.1: Tabela de dupla entrada ou contingência
Desta notação e disposição dos dados derivamos as seguintes fórmulas estatísticas.
- \(n_{ij}\) : Distribuição de frequência conjunta;
- \(n_{i+} = \sum_{j=1}^ln_{ij}\) : Total das linhas. Distribuição de frequência marginal de \(X\)
- \(n_{+j} = \sum_{i=1}^k n_{ij}\) : Total das colunas. Distribuição de frequência marginal de \(Y\)
- \(n = \sum_{i=1}^k n_{i+} = \sum_{j=1}^l n_{+j} = \sum_{i=1}^j \sum_{i=1}^l n_{ij}\) : Total geral, soma de todos os valores
- \(f_{i|j}^{X|Y} = \frac{n_{ij}}{n_{+j}}\) : Distribuição de frequência condicional de \(X\) dado que \(Y=y_j\)
- \(f_{i|j}^{X|Y} = \frac{n_{ij}}{n_{+j}}\) : Distribuição de frequência condicional de \(Y\) dado que \(X=x_i\)
- \(f_{ij} = \frac{n_{ij}}{n}\) : Distribuição de frequência relativa conjunta de \(X\) e \(Y\)
- \(f_{i+} = \sum_{j=1}^{l} f_{ij}\) : Distribuição de frequência relativa marginal de X
- \(f_{+j} = \sum_{i=1}^{k} f_{ij}\) : Distribuição de frequência relativa marginal de Y
- \(f_{i|j}^{X|Y} = \frac{f_{ij}}{f_{+j}}\) : Distribuição de frequência relativa condicional de \(X\) dado que \(Y=y_j\)
- \(f_{i|j}^{Y|X} = \frac{f_{ij}}{f_{i+}}\) : Distribuição de frequência relativa condicional de \(Y\) dado que \(X=x_i\)
X = escolaridade e Y = sexo do docente.
(a) qual o total de doutores?
(b) qual a frequência relativa por sexo?
(c) qual a frequência relativa por escolaridade?(d) qual a frequência relativa de pessoas do sexo feminino? (e) qual a frequência relativa de pessoas do sexo masculino que são mestres? (f) qual a frequência relativa de doutores que são mulheres?
rnp::rnp_2freq(x = base_docentes$escolaridade,
y = base_docentes$sexo,
digits = 3, percents = FALSE) %>%
knitr::kable(booktabs = TRUE, format = tb_formata,
caption = "Frequências cruzadas da escolaridade por sexo") %>%
kableExtra::kable_styling(latex_options = "hold_position")| Tipo | Classe X/Y | 1. Feminino | 2. Masculino | Total |
|---|---|---|---|---|
| fa | 1. Sem graduação | 3 | 7 | 10 |
| fa | 2. Graduação | 1848 | 2765 | 4613 |
| fa | 3. Especialização | 30579 | 41722 | 72301 |
| fa | 4. Mestrado | 73614 | 80671 | 154285 |
| fa | 5. Doutorado | 73812 | 87015 | 160827 |
| fa | Total | 179856 | 212180 | 392036 |
Solução. (a) Na tabela cruzada, doutores ficam na quinta linha, logo fixamos a linha i = 5 e fazemos a soma das colunas de 1 a 2 para sexo.
\(n_{5+} = \sum_{j=1}^2 n_{ij} = 73812 + 87015 = 160827\)
- neste caso temos
j=("1.Feminino","02.Masculino"), logo fazemos a soma das linhas fixando cada coluna.
\(n_{+1} = \sum_{i=1}^5 n_{i1} / n = 179856 / 392036 = 0.4588\)
\(n_{+2} = \sum_{i=1}^5 n_{i2} / n = 212180 / 392036 = 0.5412\)
- este caso é semelhante ao anterior.
Agora temos
i = ("1. Sem graduação","2. Graduação","3. Especialização","4. Mestrado","5. Doutorado"), varremos as linhas somando as colunas de 1 a 2.
\(n_{1+} = \sum_{j=1}^2 n_{1j} / n = 10 / 392036 = 0.0000\)
\(n_{2+} = \sum_{j=1}^2 n_{2j} / n = 4613 / 392036 = 0.0117\)
\(n_{3+} = \sum_{j=1}^2 n_{3j} / n = 72301 / 392036 = 0.1844\)
\(n_{4+} = \sum_{j=1}^2 n_{4j} / n = 154285 / 392036 = 0.3935\)
\(n_{5+} = \sum_{j=1}^2 n_{5j} / n = 160827 / 392036 = 0.4102\)
- este caso é parecido com o caso da letra a), mas agora fixando nas colunas da tabela.
j = 1. Feminino, logo precisamos apenas fixar esta coluna e tirar a frequência relativa do total das linhas.
\(n_{+1} = \sum_{i=1}^5 n_{ij} = 179856 / 392036 = 0.4588\)
- agora queremos uma frequência relativa condicional de pessoas do sexo masculino dado que são mestres. Temos que escolaridade é representado pela variável \(X\) e sexo pela variável \(Y\), assim.
\(f_{i=4|j}^{Y|X=x_4} = \frac{f_{ij}}{f_{i+}} = \frac{f_{42}}{f_{41}+f_{42}} = \frac{80671}{73614 + 80671} = 0.5229\)
- qual a frequência relativa de doutores que são mulheres?
Neste caso, queremos a frequência relativa condicional de doutores dado que são do sexo feminino.
\(f_{i|j=1}^{X|Y=y_1} = \frac{f_{ij}}{f_{+j}} = \frac{f_{51}}{f_{11}+f_{21}+f_{31}+f_{41}+f_{51}}=\frac{73812}{3+1848+30579+73614+73812}=0.4104\)
Inicialmente parece complicado se localizar na tabela de frequência e estabelecer a notação corretamente. Neste caso, uma dica é varrer visualmente a tabela sempre com a ideia de que i representa representa os índices de cada linha da variável X e j representa os índices de cada coluna da variável Y.
2.1.2 Gráficos para uma variável categórica
Além das tabelas de frequência simples também é possível complementar a análise de variáveis categóricas através de gráficos. Os mais conhecidos são os gráficos de setores (ou pizza) e os de barras. Através destes gráficos a informação fica facilmente visível e a obtenção de informações valiosas fica evidente.
2.1.2.1 Setores
tb <- rnp::rnp_freq(base_docentes$faixaIdade, sortd = FALSE)
p <- ggplot2::ggplot(tb, aes("", fr, fill = classe))
p + ggplot2::geom_bar(width = 1, size = 1, color = "white",
stat = "identity") +
ggplot2::coord_polar("y") +
ggplot2::geom_text(aes(label = paste0(round(100*fr, 1), "%")),
position = position_stack(vjust = 0.5), size=3) +
ggplot2::labs(x = NULL, y = NULL, fill = NULL, title = "") +
ggplot2::guides(fill = guide_legend(reverse = TRUE)) +
ggplot2::theme_gray() +
ggplot2::theme(axis.line = element_blank(),
axis.text = element_blank(),
axis.ticks = element_blank(),
legend.position="right",
legend.text = element_text("Classe"))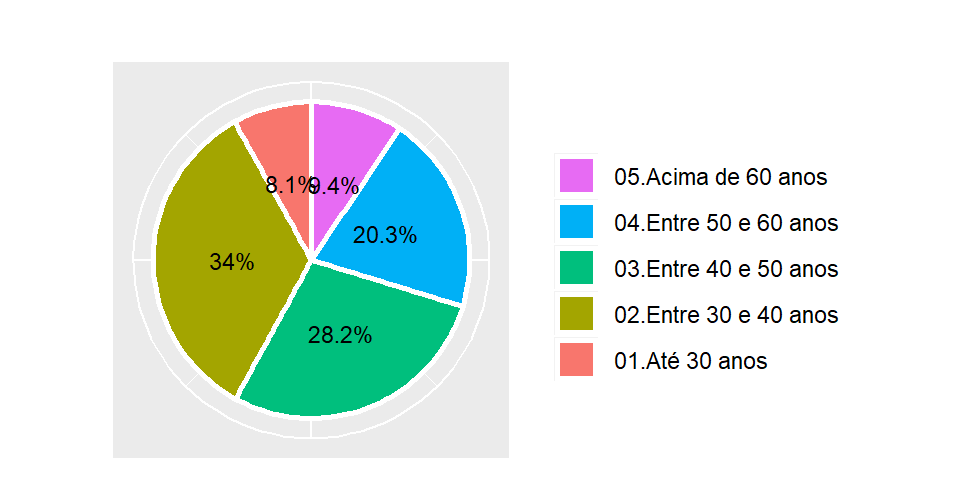
Figura 2.2: Gráfico de setores para faixa de idade dos docentes
Como podemos notar, a figura 2.2 é muito intuitiva para representar visualmente a distribuição de frequências das classes de uma variável categórica. Combinado com as cores de cada fatia, fica claro e objetivo a parcela de cada categoria para explicar o todo que por sua vez representa 100%.
2.1.2.2 Barras
Gráficos de barras também são intuitivos e geralmente são preferíveis em relação aos gráficos de setores. Isso ocorre porque o olho humano é mais sensível a linhas do que círculos e formas em 3D e prefere analisar figuras mais limpas. Para expandir seus conhecimentos sobre análise visual, sugerimos a (Tufte and Graves-Morris 2014).
p <- ggplot2::ggplot(tb, aes(classe, fr, fill = classe))
p + ggplot2::geom_bar(width = 1, size = 1, color = "white",
stat = "identity", show.legend = FALSE) +
ggplot2::geom_text(aes(label = paste0(round(100*fr, 1), "%")),
position = position_stack(vjust = 1), size=3) +
ggplot2::labs(x = NULL, y = NULL, fill = NULL, title = "") +
ggplot2::theme_gray() + coord_flip() +
ggplot2::theme(axis.line = element_blank())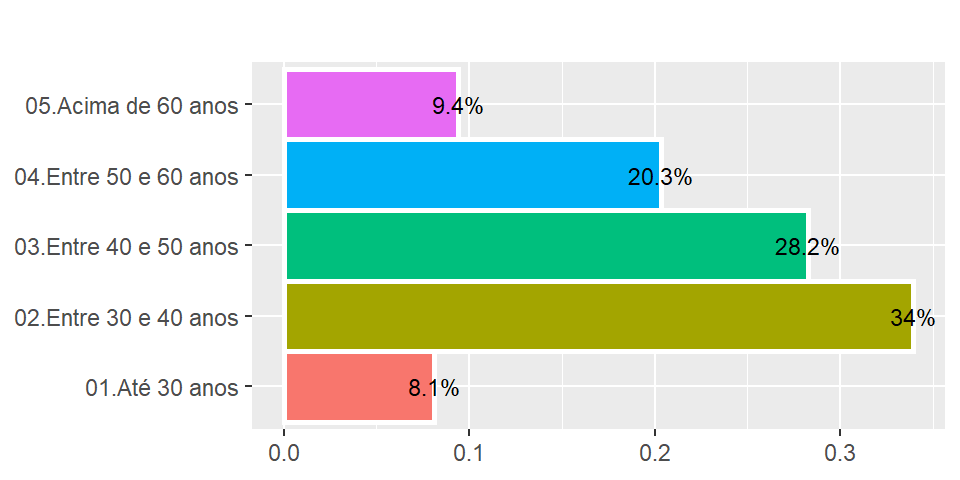
Figura 2.3: Gráfico de barras para faixa de idade dos docentes
A figura 2.3 mostra um gráfico de barras para as faixas de idade dos docentes, nele pode-se notar que visualmente as diferenças de patemares ficam evidentes. Com isso a leitura fica mais direta e é possível comparar todas as barras simultaneamente. O eixo x contém as proporções e o eixo y a descrição de cada categoria nesta visão horizontal.
2.1.3 Gráfico para duas variáveis categóricas
Vimos nas tabelas de frequência que as tabelas de dupla entrada são boas ferramentas para analisar conjuntamente a relação entre duas variáveis, mas isso também pode ser feito de forma visual.
2.1.3.1 mosaicplot
Podemos visualizar a relação entre duas variáveis categóricas ou numéricas de poucas classes, através do Gráfico de mosaico (mosaic plot). O pacote ggmosaic expande o ggplot2 para produzir este tipo de gráfico.
p <- ggplot2::ggplot(base_docentes)
p + ggplot2::theme_gray() +
ggmosaic::geom_mosaic(aes(x = product(sexo), fill = faixaIdade),
show.legend = FALSE) +
ggplot2::labs(x = NULL, y = NULL, fill = NULL, title = "") +
ggplot2::theme(axis.line = element_blank())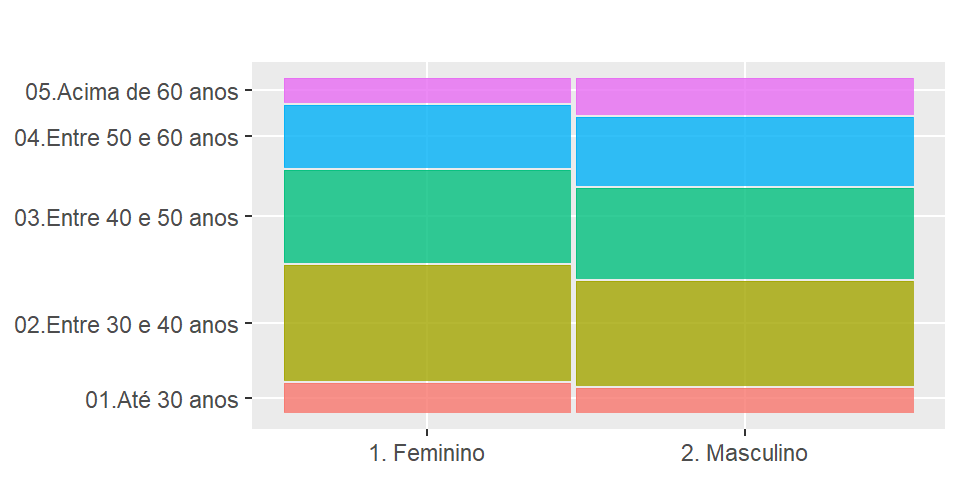
Figura 2.4: Gráfico de mosaico para faixa de idade dos docentes por sexo
Cada coluna da figura 2.4 representa uma classe da variável sexo do docente e cada linha representa uma classe da variável faixa de idade. Note que o cruzamento entre linhas e colunas geram retângulos com a proporção de cada cruzamento, sendo maior nos casos em que existem mais dados. Por exemplo, proporcionalmente docentes do sexo masculino acima de 60 anos são maioria neste conjunto de dados.
2.1.4 Exercícios
Para resolver os exercícios desta seção, utilize o conjunto de dados DM_CURSO.CSV presente na pasta de dados ou no pacote ?rnp::dm_curso. Esta base de dados possui informações sobre os cursos das IES no censo de 2017 do INEP. Mais informações sobre as variáveis podem ser obtidas no dicionario de dados presente na pasta AJUDA/ANEXOS ou no site do INEP.
## Observations: 35,693
## Variables: 10
## $ NU_ANO_CENSO <int> 2017, 2017, 2017, ...
## $ CO_IES <int> 789, 4567, 2341, 6...
## $ CO_LOCAL_OFERTA <int> 1033528, 659871, 1...
## $ CO_UF <int> 14, 51, 35, 35, 53...
## $ CO_MUNICIPIO <int> 1400100, 5107925, ...
## $ CO_CURSO <int> 1259131, 1258115, ...
## $ NO_CURSO <chr> "MÚSICA", "GESTÃO ...
## $ CO_OCDE_AREA_GERAL <int> 1, 3, 3, 5, 3, 7, ...
## $ CO_OCDE_AREA_ESPECIFICA <int> 14, 34, 38, 52, 38...
## $ CO_OCDE_AREA_DETALHADA <int> 146, 345, 380, 522...DESC_TP_CATEGORIA_ADMINISTRATIVA e responda qual a taxa de cursos por IES tipo pública.
rnp::rnp_freq(base_curso$DESC_TP_CATEGORIA_ADMINISTRATIVA, digits = 3) %>%
knitr::kable(booktabs = TRUE, format = tb_formata,
caption = "Frequências categoria administrativa") %>%
kableExtra::kable_styling(latex_options = "hold_position")| classe | fa | fr | Faa | Fra |
|---|---|---|---|---|
| 1. Pública Federal | 6538 | 0.183 | 6538 | 0.183 |
| 2. Pública Estadual | 3558 | 0.100 | 10096 | 0.283 |
| 3. Pública Municipal | 502 | 0.014 | 10598 | 0.297 |
| 4.Privada com fins lucrativos | 12488 | 0.350 | 23086 | 0.647 |
| 5. Privada sem fins lucrativos | 12523 | 0.351 | 35609 | 0.998 |
| 7. Especial | 84 | 0.002 | 35693 | 1.000 |
DESC_TP_CATEGORIA_ADMINISTRATIVA e interprete quais as categorias de maior e menor influência.
# Primeiro fazemos as frequências, depois o gráfico
tb <- rnp::rnp_freq(base_curso$DESC_TP_CATEGORIA_ADMINISTRATIVA)
p <- ggplot2::ggplot(tb, aes(classe, fr, fill = classe))
p + ggplot2::geom_bar(width = 1, size = 0.6, color = "white",
stat = "identity", show.legend = FALSE) +
ggplot2::geom_text(aes(label = paste0(round(100*fr, 1), "%")),
position = position_stack(vjust = 1), size=3) +
ggplot2::labs(x = NULL, y = NULL, fill = NULL, title = "") +
ggplot2::theme_gray() + coord_flip() +
ggplot2::theme(axis.line = element_blank())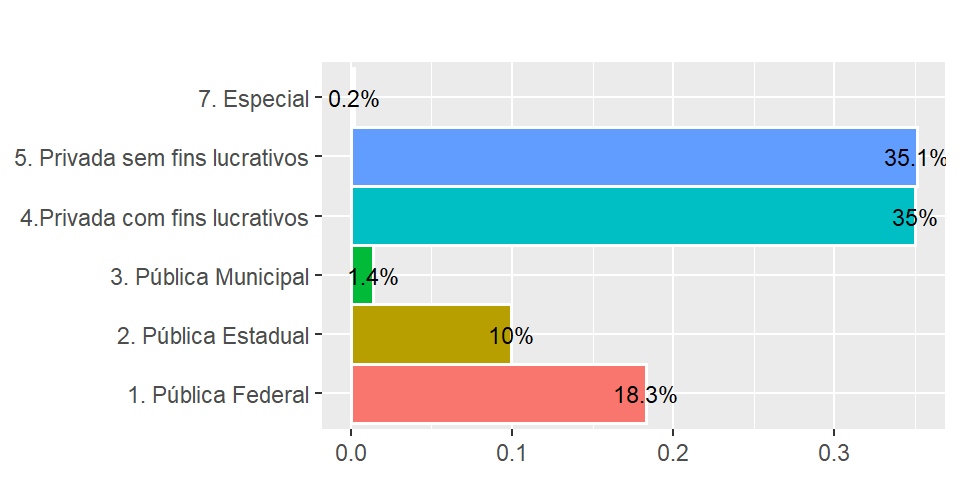 As categorias privada com e privada sem fins lucrativos representam 70,1% dos dados, sendo as mais representativas. Públicas municipais são minoria (1,4%) e especial apenas (0.2%). Temos indícios de que políticas públicas para aumentar a participação de cursos especiais devem ser melhoradas.
As categorias privada com e privada sem fins lucrativos representam 70,1% dos dados, sendo as mais representativas. Públicas municipais são minoria (1,4%) e especial apenas (0.2%). Temos indícios de que políticas públicas para aumentar a participação de cursos especiais devem ser melhoradas.
DESC_TP_GRAU_ACADEMICO responda quais as categorias de maior e menor ocorrências de cursos. Desconsidere a categoria missing.
# As categorias diferentes de missing são:
# 1. Bacharelado, 2. Licenciatura e 3. Tecnológico
# missing representam 0.09% dos dados.
grau <- c("1. Bacharelado", "2. Licenciatura", "3. Tecnológico")
GrauAcad <- base_curso %>%
dplyr::transmute(GrauAcad = DESC_TP_GRAU_ACADEMICO) %>%
dplyr::filter(GrauAcad %in% c("1. Bacharelado",
"2. Licenciatura",
"3. Tecnológico"))
tb <- rnp::rnp_freq(GrauAcad$GrauAcad, digits = 3)
p <- ggplot2::ggplot(tb, aes(classe, fr, fill = classe))
p + ggplot2::geom_bar(width = 1, size = 0.6, color = "white",
stat = "identity", show.legend = FALSE) +
ggplot2::geom_text(aes(label = paste0(round(100*fr, 1), "%")),
position = position_stack(vjust = 1), size=3) +
ggplot2::labs(x = NULL, y = NULL, fill = NULL, title = "") +
ggplot2::theme_gray() + coord_flip() +
ggplot2::theme(axis.line = element_blank())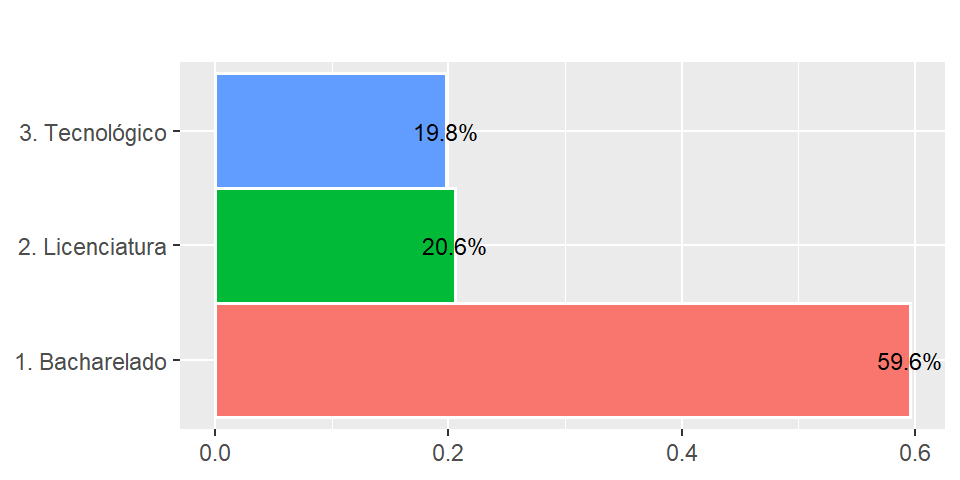
Como o gráfico mostra, 59,6% dos cursos são de bacharelado frente a 20,6% de licenciatura. Estamos formando poucos professores?
DESC_TP_GRAU_ACADEMICO em um gráfico de barras e interprete os resultados para cursos tecnologicos em relação aos cursos de licenciatura.
DESC_TP_ORGANIZACAO_ACADEMICA descreve características do tipo de organização, estude esta variável graficamente.
DESC_IN_POSSUI_LABORATORIO e DESC_TP_CATEGORIA_ADMINISTRATIVA para verificar a existência de laboratórios nos cursos públicos e privados.
2.2 Variáveis numéricas
Variáveis numéricas são se longe o tipo mais comum e analisável de dado, pois contemplam medidas de processos diversos. Por exemplo, idade de uma pessoa em dias, peso, altura, total de pessoas em um metrô, em uma fila de cinema e por aí vai. Por permitir cálculos estatísticos, este tipo de variável tem sido estudado há milênios e portanto, boa parte das técnicas estatísticas atuais de baseiam em dados numéricos. Neste tópico abordaremos as principais medidas estatísticas cobrindo centralidade, dispersão entre outras e os principais gráficos que podem ser empregados.
2.2.1 Medidas estatísticas de centralidade
Quando olhamos um conjunto de dados de uma variável numérica logo pensamos em alguma forma de resumir estes dados para gerar algum tipo de informação. As medidas estatísticas de centralidade representam resumos numéricos que apontam para o centro do conjunto de dados. A figura 1.7 ilustra a ideia e também indica uma vulnerabilidade da média que são os extremos. Pontos extremos podem inserir viés no valor e na interpretação de uma média, mas para complementar a média temos a mediana, moda e quartis que veremos nos tópicos a seguir.

Figura 2.5: Na média, tudo bem
As medidas estatísticas descritas nesta seção são aplicadas a conjuntos de dados (amostras e populações) e também a distribuições de probabilidade. Para manter o teor prático deste texto, vamos focar em dados. No capitulo sobre probabilidade retornaremos o assunto no contexto das distribuições de probabilidade.
2.2.1.1 Média (\(\bar X, \mu\))
Existem muitos tipos de média e entre elas temos a média aritmética, média ponderada, média geométrica e a média harmônica. Em qualquer uma delas, o intuito é resumir a centralidade dos dados em relação a seus extremos dando nenhum, mais ou menos peso para cada observação. Representamos a média aritmética de uma amostra pela letra latina \(\bar X\) (xis-barra) e a média populacional pela letra grega \(\mu\) e calculamos com a mesma expressão matemática.
Veremos no capítulo sobre teoria das probabilidades que a média de uma variável aleatória \(X\) é chamada de valor esperado ou esperança de \(X\) e geralmente é definido por \(E[X]\).
Média aritmética: é a soma de todos os valores e dividido pelo total deles. Ou seja, o resultado dessa divisão equivale a um valor médio entre todos os valores e é calculada por:
\[\bar X = \frac{x_1 + x_2 + x_3 + \dots + x_n}{n}, i = 1, 2, 3, \dots, n\]
onde \(x_1, x_2, x_3, \dots, x_n\) representam cada valor correspondente a um elemento \(i\) da amostra e \(n\) o total de elementos.
Este tipo de média é aplicado preferencialmente quando cada elemento tem peso igual a uma unidade, ou seja, quando não houver muita repetição.
base_ies %>%
dplyr::mutate(Sigla = SG_IES,
TotalTecnicos = QT_TEC_TOTAL,
ReceitaPropria = VL_RECEITA_PROPRIA,
DespesaPesquisa = VL_DESPESA_PESQUISA) %>%
dplyr::summarise("Total técnicos" = mean(TotalTecnicos),
"Receita própria" = mean(ReceitaPropria),
"Repesa pesquisa" = mean(DespesaPesquisa)) %>%
knitr::kable(caption = "Média anual para dados de IES",
format = tb_formata) %>%
kableExtra::kable_styling(latex_options = "hold_position")| Total técnicos | Receita própria | Repesa pesquisa |
|---|---|---|
| 168.1 | 145378180 | 886404 |
A tabela 2.5 mostra que a média da receita própria anual das IES brasileiras, segundo o censo de 2017, foi de R$ 143.468.742. Este valor parece um pouco suspeito, pois representa 85,76% do PIB (Produto Interno Bruto) do estado de pernambuco tendo 2018 como ano base, segundo dados do IBGE. Mas vamos entender adiante como investigar isso melhor.
Média aritmética ponderada: Neste caso, é assumido que cada elemento amostral tem um peso, então a média aritmética ponderada é calculada multiplicando cada valor do conjunto de dados pelo seu peso, somando tudo e dividindo pela soma de todos os pesos. Na verdade a média aritmética simples é um caso especial da ponderada quando cada peso vale 1. A média ponderada é dada por:
\[\bar X_p = \frac{p_1 \times x_1 + p_2 \times x_2 + p_3\times x_3 + \dots + p_n \times x_n}{p_1 + p_2 + p_3 + \dots + p_n}, i = 1, 2,3 \dots, n\]
sendo \(x_1, x_2, x_3, \dots , x_n\) cada valor associado a um \(i-ésimo\) elemento da amostra e \(p_1 + p_2 + p_3 + \dots + p_n\) cada peso relacionado com cada elemento da amostra.
Quando a amostra possuir muitas repetições ou precisar ser balizada por algum peso, esta média é mais recomendada.
base_ies %>%
dplyr::mutate(TotalTecnicos = QT_TEC_TOTAL,
ReceitaPropria = VL_RECEITA_PROPRIA) %>%
dplyr::summarise("Receita" = mean(ReceitaPropria),
"Receita ponderada" =
weighted.mean(x = ReceitaPropria,
w = TotalTecnicos)) %>%
knitr::kable(format = tb_formata,
caption = "Média receita própria
ponderada pelo total de técnicos") %>%
kableExtra::kable_styling(latex_options = "hold_position")| Receita | Receita ponderada |
|---|---|
| 145378180 | 229043797 |
Note da tabela 2.6, que a média ponderada é maior que a aritmética da tabela 2.5 e isso ocorre porque IES maiores possuem mais receita e sendo esta ponderada por um volume maior de técnicos faz com que a média suba.
A média geométrica é mais rara, porém existem aplicações nas ciências sociais como formas de estimar a expectativa de vida ao nascer, na economia como indicadores financeiros e na geometria. Assim como a média geométrica, a harmônica também é rara e possui aplicações na área da física em situações que envolvem taxas. Fica ao cargo do leitor interessado pesquisar mais sobre estes casos especiais de médias.
2.2.1.2 Mediana (\(M_d\))
Para compreender melhor o conceito de mediana é importante saber que ela depende da ordenação de forma crescente dos dados da variável numérica. Como se trata de números, ao ordenar os dados podemos trazer a ideia de centro. A mediana é uma medida estatística que calcula o valor central dos dados de forma que se tenha metade dos valores (50%) abaixo e metade acima da mediana. Resumindo, mediana é o valor do meio do conjunto de dados.
Quando o conjunto de dados tiver um número impar de observações, a mediana será o valor central e quando o comprimento for par, a mediana será a média dos dois elementos centrais. A mediana também é conhecida como uma medida resistente a pontos discrepantes e como segundo quartil \(Q_2\).
c(0, 1, 2, 3, 4, 5, 6) qual é a mediana?
Neste caso a mediana é 3, porque a amostra tem tamanho 7 (impar) e 3 é o elemento que separa os dados 50% / 50%. No R utilizamos a função median() para calcular a mediana.
## [1] 3c(2, 3, 4, 5, 6, 7) qual é a mediana?
Neste caso a mediana é \(\frac{4 + 5}{2} = 4.5\), porque a amostra tem tamanho 6 (par) sendo que 4 e 5 são os elementos que estão no centro.
## [1] 4.52.2.1.3 Moda (\(M_o\))
A moda é uma medida estatística que aponta valor(es) mais frequente(s) numa amostra com elementos repetidos, sendo ela o valor ou conjunto de valores mais comuns. Quando os dados são numéricos e já estão agrupados em classes, chamamos a classe com maior frequência de classe modal e seu valor é determinado pela média dos seus extremos.
Diferentemente da média e mediana já vistas, a moda também se aplica a variáveis categóricas, uma vez que serve para identificar as classes ou valores mais frequentes.
Quando uma amostra possui apenas uma moda diz-se que ele é unimodal, sem tem duas é bimodal e se tem três ou mais é dita multimodal.
rnp::rnp_freq() para determinar as faixa de idade. Por padrão esta função trabalha com quartis para categorizar dados numéricos.
knitr::kable(rnp::rnp_freq(base_docentes$idade),
digits = 3,
booktabs = TRUE,
format = tb_formata,
caption = "Frequências para idade dos docentes das IES") %>%
kableExtra::kable_styling(latex_options = "hold_position")| classe | fa | fr | Faa | Fra |
|---|---|---|---|---|
| 19–36 | 107295 | 0.274 | 107295 | 0.274 |
| 36–43 | 95550 | 0.244 | 202845 | 0.517 |
| 43–52 | 92360 | 0.236 | 295205 | 0.753 |
| 52–99 | 96831 | 0.247 | 392036 | 1.000 |
Na tabela 2.7 vemos que a classe modal é a que contém idades entre 19 e 36 anos, pois ela representa 27,4% da amostra. Com base na classe modal, temos que \(M_o = \frac{19+36}{2} = 27,5\) anos.
x = {2, 5, 3, 4, 4}, y = {5,5,7,7,6,1,2,1}, z = {9,1,7,8,4} determine, quando existir e moda e sua classificação.
table() e duplicated(). Enquanto a primeira faz uma tabulação dos valores ou das classes, a segunda varre a variável buscando quem são os valores que ocorrem mais de uma vez e retornando TRUE, caso algum se repita. Vejamos a solução.
# Preparando os dados como vetores através da função c() e
# ordenando com sort()
x <- sort(c(2, 5, 3, 4, 4))
paste("x possui", x[duplicated(x)], "como moda")## [1] "x possui 4 como moda"## [1] "y possui 1 como moda" "y possui 5 como moda"
## [3] "y possui 7 como moda"## [1] "z possui como moda"As medidas de centralidade de forma geral sempre buscarão representar quais dados estão no centro ou apontando para mesmo no conjunto de dados. A figura 2.6 exemplifica um conjunto de medidas em uma linha onde a média representa o centro e os pontos as possíveis medidas realizadas.
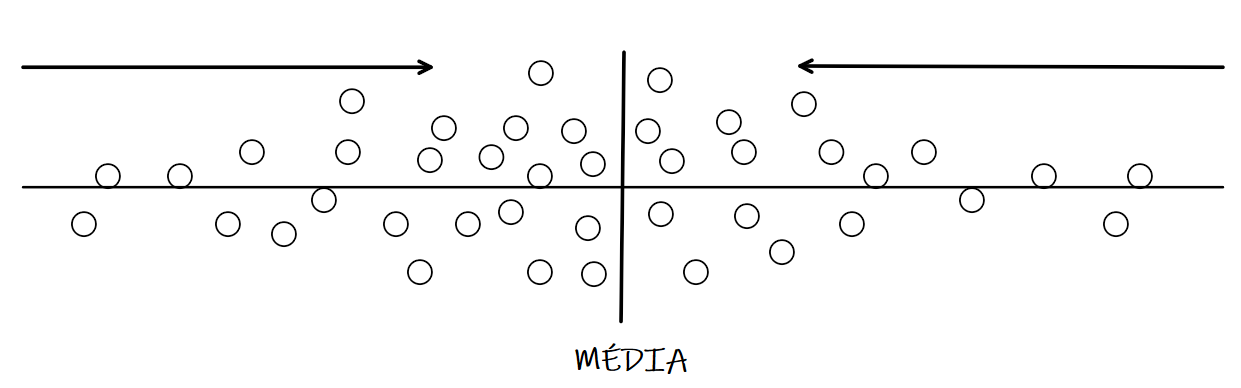
Figura 2.6: Centralidade
O centro de massa é onde ocorre a maioria das observações e é nesta região que geralmente a média será encontrada.
2.2.1.4 Exercícios
Utilize a base de dados das IES para responder à questão a seguir.
QT_TEC_MEDIO_FEM, QT_TEC_MEDIO_MASC, QT_TEC_SUPERIOR_FEM e QT_TEC_SUPERIOR_MASC.
mean() e median() com auxílio das funções lapply() do R base e summarise() do pacote dplyr.
variaveis <- c("QT_TEC_MEDIO_FEM", "QT_TEC_MEDIO_MASC",
"QT_TEC_SUPERIOR_FEM", "QT_TEC_SUPERIOR_MASC")
tb <- sapply(variaveis, function(i) {
base_ies %>%
select(i) %>%
summarise("Média" = round(mean(.[[i]], na.rm = TRUE), 2),
"Mediana" = round(median(.[[i]], na.rm = TRUE),2))
}) %>%t()
knitr::kable(tb, booktabs = TRUE, format = tb_formata,
caption = "Média e mediana técnicos (IES)") %>%
kableExtra::kable_styling(latex_options = "hold_position")| Média | Mediana | |
|---|---|---|
| QT_TEC_MEDIO_FEM | 27.26 | 6 |
| QT_TEC_MEDIO_MASC | 27.51 | 4 |
| QT_TEC_SUPERIOR_FEM | 27.87 | 6 |
| QT_TEC_SUPERIOR_MASC | 20.37 | 3 |
A tabela mostra que em média, as IES possuem 27 técnicos de nível médio, masculino ou feminino com mediana de 6 para feminino e 4 para masculino. Isso significa que cerca de 50% das IES possuem até 10 (6 + 4) técnicos de nível médio. Para os técnicos de nível superior, a média feminina é superior em quase 8, sendo de 27,87 contra 20,37 dos masculinos. A mediana de mulheres se iguala àquelas com curso técnico.
2.2.2 Medidas estatísticas de dispersão
De forma simples, podemos entender medidas de dispersão como estatísticas que medem o quanto os dados estão espalhados. Desta forma, este tipo de medida é zero se os dados são todos iguais e vai aumentando à medida em que a diversidade dos dados aumenta. Estatísticas de dispersão são muito aplicadas em área como física ajudando a medir a variabilidade de medições feitas em experimentos; nas ciências biológicas estimando a variabilidade interindivíduos (membros distintos da mesma amostra são diferentes uns dos outros) e intraindivíduos (um mesmo individuo submetido a algum teste em condições distintas produzem resultados diferentes) e em muitos ramos das ciências como economia, medicina e engenharia. As principais medidas estatísticas de dispersão são desvio padrão (\(S,\sigma\)) e variância (\(S^2,\sigma^2\)), amplitude, desvio absoluto e coeficiente de variação
2.2.2.1 Desvio padrão (\(S,\sigma\)) e variância (\(S^2,\sigma^2\))
Desvio padrão e variância são medidas que buscam estimar a dispersão dos dados em torno da sua média. Quando estamos falando de população temos desvio padrão e variância populacionais. Representados pela letra grega minúscula \(\sigma\) o desvio padrão e \(\sigma^2\) para a variância. No caso de amostra, representamos com a letra latina \(S\) o primeiro e \(S^2\) para o segundo caso.
O desvio padrão populacional é dado por:
\[{\displaystyle \sigma ={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}(X_{i}-\mu )^{2}}}}\]
em que \(X_i,i=1,2,...,N\) são os elementos da população e \(\mu\) é a média populacional.
Já o desvio padrão amostral é dado por:
\[{\displaystyle S_{n-1}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}}}}\]
em que \(X_i,i=1,2,...,n\) são os elementos da amostra e \(\bar X\) é a média amostral.
Note que o denominador do desvio padrão amostral é \((n-1)\) em vez de \(n\). Este fator de correção é conhecido como correção de Bessel (Reichmann 1961) e é aplicado porque no cálculo da média a partir da amostra, perde-se um grau de liberdade. Grau de liberdade refere-se ao total de elementos da amostra supondo que cada um é independente do outro. Como \(S\) utiliza \(\bar X\) que por sua vez está ligada com cada elemento da amostra, há epenas \(n-1\) elementos independentes após \(\bar X\) ser calculado.
A variância é o quadrado do desvio padrão. Assim:
Variância populacional é dada por
\[\sigma^2 ={{\frac {1}{N}}\sum _{i=1}^{N}(X_{i}-\mu )^{2}}\]
e a variância amostral por:
\[S_{n-1}={{\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}}\]
Em R calculamos o desvio padrão de uma variável com a função sd() e a variância com a função var().
base_docentes %>%
dplyr::summarise(`Média` = mean(idade),
`Desvio padrão` = sd(idade),
`Variância` = var(idade))## Média Desvio padrão Variância
## 1 44.53 10.96 120.2ou diretamente com.
## [1] "Média = 44.531"## [1] "Desvio padrão = 10.963"## [1] "Variância = 120.181"- Interpretação do desvio padrão: No exemplo acima, vemos que a média de idade dos docentes é de 44,53 anos com desvio padrão de 10,96 e variância de 120,20, mas o que isso significa? - A variância de idade é uma medida cuja unidade de media é \(ano^2\). Ano ao quadrado não tem interpretação direta então utilizamos o desvio padrão. Em geral quanto maior o desvio padrão mais espalhados estão os dados em relação à media. Não é conhecida uma regra generalizada para dizer se um desvio padrão é menor ou maior, porém, com base na teoria das probabilidades temos uma regra de ouro que é aplicada sempre que a curva dos dados segue uma distribuição Normal (por hora, epenas aceite, veremos ela mais adiante!).
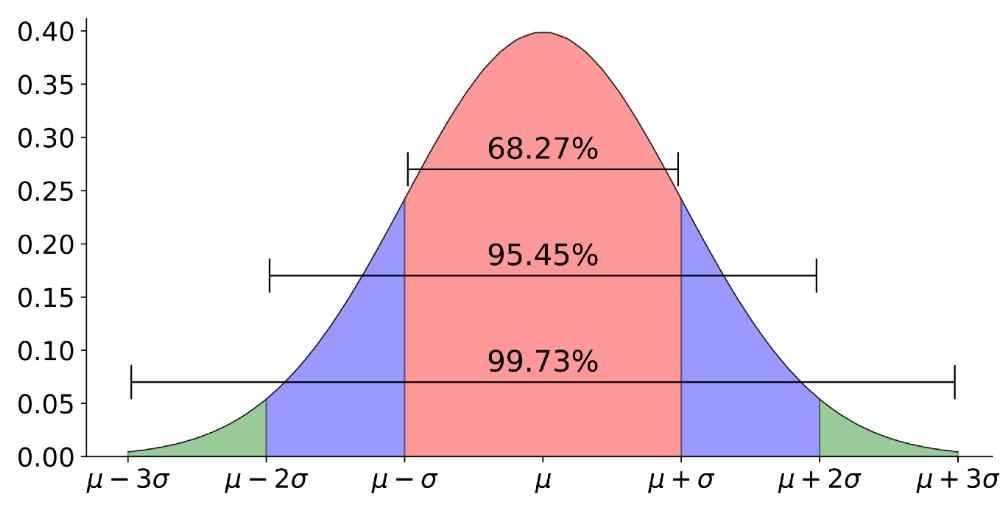
Figura 2.7: Centralidade
Conforme vemos na figura 2.7, em torno da média mais ou menos um desvio padrão devem estar 68,27% dos dados, já entre a média mais ou menos 2 desvios padrão devem estar 95,45% dos dados. Seguindo esta lógica, a interpretação deve levar em conta a distribuição dos dados e a precisão que o experimento ou estudo exige. Assim, sendo no nosso exemplo a média de idade dos docentes é 44,2 então 68,27% dos docentes devem possuir idades na faixa de \(44,2 \pm 11 = (33.4-55.4)\) anos.
2.2.2.2 Amplitude
A amplitude de um conjunto de dados ordenado é a distância entre o menor e o maior valor. Na figura 2.6 se seus valores estiverem ordenados do maior para o menor, a amplitude será o ponto mais à direita Máximo menos o ponto mais à esquerda Mínimo.
Representamos um conjunto de dados ordenado da seguinte forma, em que o subscrito representa a ordem da observação.
\[X_{(1)}\leq X_{(2)}\leq X_{(3)}\leq \cdots \leq X_{(n-1)}\leq X_{(n)}\] Assim, sendo podemos expressar a amplitude ou range por
\[R = X_{(n)} - X_{(1)} = Max(X) - Min(X)\]
# Ordenando os dados do menor para o maior
idade <- sort(base_docentes$idade, decreasing = FALSE)
# obtendo o menor e o maior valor
menor <- idade[1]
maior <- idade[length(idade)]
R1 <- maior - menor
# ou pelo minimo e máximo dos dados
R2 <- max(idade) - min(idade)
paste("As duas medidas são iguais?", all.equal(R1,R2))## [1] "As duas medidas são iguais? TRUE"## [1] 80 802.2.2.3 Coeficiente de variação \(cv\)
Esta medida estatística muitas vezes é chamada de desvio padrão relativo e é uma medida padronizada de dispersão. Em alguns contextos é possível optar pelo cv ao invés do desvio padrão. Quanto maior for o coeficiente de variação, maior será a dispersão nos dados em torno da média. O cv é expresso como a divisão entre o desvio padrão e a média e pode ser calculado pela seguinte expressão.
\[cv_{amostral} = \frac{S}{\bar X}\]
e
\[cv_{populacional} = \frac{\sigma}{\mu}\]
Vale salientar que o cv e o desvio padrão se aplicam a dados estritamente positivos.
- Interpretação: por ser uma medida adimensional, o cv é uma medida prática para comparar e interpretar a variabilidade entre dois conjuntos de dados de tipos diferentes e pode ser interpretada em termos percentuais. Veja o exemplo a seguir.
base_ies %>%
dplyr::summarise(`Média receita` = mean(VL_RECEITA_PROPRIA),
`Média técnicos` = mean(QT_TEC_TOTAL),
`CV receita` = c(sd(VL_RECEITA_PROPRIA) /
mean(VL_RECEITA_PROPRIA)),
`CV técnicos` = sd(QT_TEC_TOTAL) / mean(QT_TEC_TOTAL)) %>%
round(., digits = 3)## Média receita Média técnicos CV receita CV técnicos
## 1 145378180 168.1 2.867 3.475Os cálculos mostram uma enorme variabilidade dos dados das IES, pois o cv para receita é 286% e para total de técnicos é 347%. Neste caso, temos indicativos de que a dispersão dos dados é grande. Isso pode ser explicado pelo tamanho das IES. Por exemplo, as federais são minoria na base de dados, mas possuem grande quantidade de técnicos e alto aporte de receita, enquanto as IES menores, geralmente privadas possuem menor número de técnicos e menor receita. Estados como São Paulo apresentam números muito grandes em relação ao restante do país.
2.2.3 Outras medidas
Existem muitas estatísticas úteis para analisar dados numéricos que nem sempre são exploradas, entre elas temos os quartis, decis, percentis e amplitude interquartis.
2.2.3.1 Quartis, decis e percentis
- Quartis: Chamamos de quartil qualquer uma das três medidas que separam um conjunto de dados ordenado em q partes iguais. Quartil vem de 1/4 (um quarto dos dados). A mediana que já vimos representa o segundo quartil. Costumamos representar os quatis pela letra Q seguida de um número tais como:
\(Q1\): primeiro quartil representa 25% da amostra ordenada;
\(Q2\): segundo quartil ou mediana representa 50% da amostra ordenada;
\(Q3\): terceiro quartil representa 75% da amostra ordenada;
Decil: O raciocínio é o mesmo dos quatis. Decis são medidas que dividem o conjunto de dados em 10 partes iguais. O primeiro decil representa 10% dos dados, o segundo 20% e assim por diante.
Percentil: De forma análoga aos decis, os percentis dividem o conjunto de dados em 100 partes iguais.
Para obter estas estatísticas seguimos o mesmo racional da mediana, dividindo os dados em partes iguais e identificando os elementos do centro e borda. No R podemos calcular facilmente estas estatísticas pela função quantile() para qualquer tamanho de faixa e por summary() para os quartis. Sempre que desejar fazer um raio-x dos dados é sugerido fazer uma análise de quartil, decil ou percentil, pois desta forma ficará evidente qualquer anomalia nos dados.
2.2.3.2 Amplitude interquartil
A amplitude interquartil ou do inglês InterQuartile Range (IQR) é a medida de distância ou range entre o primeiro quartil \(Q_1\) e o terceiro \(Q_3\). Sua importância reside no fato de que ela representa os 50% dos dados centrais do conjunto de dados.
\[IQR = Q_3-Q_1\]
Junto com esta estatística surge também dois conceitos importantes que são os limites superiores \(LS\) e inferiores \(LI\) para decidir se determinado ponto é discrepante ou não. Uma dada medida é dita discrepante ou outlier quando ela está muito diferente da maioria das medidas realizadas. É demonstrado que no intervalo determinado por \(LI=Q_1-1.5 \times IQR\) e \(LS=Q_3+1.5 \times IQR\) temos 99% dos dados, assim qualquer valor que cair fora deste intervalo em geral, pode ser chamado de outlier.
base_docentes %>%
dplyr::summarise(Q1 = quantile(idade, probs = 0.25),
Q2 = quantile(idade, probs = 0.50),
Q3 = quantile(idade, probs = 0.75),
IQR = Q3 - Q1,
LI = Q1 - 1.5*IQR,
LS = Q3 + 1.5*IQR,
Noutliers = sum(idade > LS),
Ntotal = n(),
Pct = Noutliers / Ntotal) ## Q1 Q2 Q3 IQR LI LS Noutliers Ntotal Pct
## 1 36 43 52 16 12 76 951 392036 0.002426Conforme a analise acima, vemos que apenas \(\frac{951}{392036} = 0,24\%\) dos docentes são outliers possuindo idade acima de 76 anos.
Outliers possuem grande importância na estatística e nunca devem ser negligenciados, pois podem trazer informação valiosa para a análise. Existem muitas técnicas de detecção de outliers mais robustas que esta que vimos a partir dos quartis. Ao leitor interessado ver (Barnett and Lewis 1974) e para uma visão baseada em R ver (Komsta 2011).
2.2.3.3 Os cinco números
Os cinco números são um conjunto de estatísticas composto por \(Min, Q_1,Q_2,Q_3\) e \(Max\), estas cinco estatísticas costumam ser suficientes para analisar a distribuição dos dados pois junta as estatísticas mais importantes, a mediana representando uma medida de centralidade, os quartis \(Q1,Q3\) representado medidas de dispersão e o mínimo e máximo que representam o range dos dados.
É comum em estatística, juntarmos em uma tabela as principais estatísticas de uma variável numérica para interpretar sua relevância no contexto do estudo ou experimento em questão. Além do resumo dos cinco números, podemos adicionar outras estatísticas de nosso interesse. A função rnp_summary() em conjunto com rnp_freq() e rnp_summary_by() nos auxiliarão em muitas análises no curso deste livro.
2.2.3.4 Exercícios
Ainda na base das IES, analise através de estatísticas de dispersão as questões a seguir.
VL_DESPESA_PESSOAL_DOCENTE. Interprete estatísticas de dispersão para esta variável.
estatisticas <- c("Min","Q1","Media","Mediana","Q3","Max","cv")
tb <- rnp::rnp_summary(base_ies$VL_DESPESA_PESSOAL_DOCENTE)[estatisticas]
knitr::kable(t(tb), booktabs = TRUE, format = tb_formata, digits = 3,
caption = "ex: Média e mediana técnicos (IES)") %>%
kableExtra::kable_styling(latex_options = "hold_position")| Min | Q1 | Media | Mediana | Q3 | Max | cv |
|---|---|---|---|---|---|---|
| 1 | 696484 | 66328326 | 3295507 | 37257632 | 7600039210 | 3.661 |
NO_IES e VL_RECEITA_PROPRIA ordenada da maior para a menor.
base_ies %>%
dplyr::transmute(NomeIES = NO_IES, ReceitaPropria = VL_RECEITA_PROPRIA) %>%
dplyr::arrange(desc(ReceitaPropria)) %>%
head(n = 10) %>%
knitr::kable(booktabs = TRUE, format = tb_formata, digits = 3) %>%
kableExtra::kable_styling(latex_options = "hold_position")| NomeIES | ReceitaPropria |
|---|---|
| FACULDADE DE ADMINISTRAÇÃO, CIÊNCIAS, EDUCAÇÃO E LETRAS | 6248050290 |
| FACULDADE MAURÍCIO DE NASSAU DE MOSSORÓ | 4434457964 |
| FACULDADE MAURÍCIO DE NASSAU DE MACEIÓ | 4024118925 |
| Faculdade Fernanda Bicchieri | 4000452319 |
| FACULDADE ESTÁCIO DE SÁ DE VILA VELHA | 3131607366 |
| FACULDADE ESTÁCIO DE SÁ DE CAMPO GRANDE | 3131607366 |
| FACULDADE ESTÁCIO DE SÁ DE GOIÁS | 3131607366 |
| CENTRO UNIVERSITÁRIO ESTÁCIO JUIZ DE FORA - ESTÁCIO JUIZ DE FORA | 3131607366 |
| UNIVERSIDADE ESTÁCIO DE SÁ | 3131607366 |
| FACULDADE ESTÁCIO DE SÁ DE OURINHOS | 3131607366 |
2.2.4 Gráficos para uma variável numérica
Existem muitos tipos de gráficos, porém para uma variável listamos os três que consideramos mais importantes.
2.2.4.1 Histogramas
Os histogramas são um tipo de gráfico de barras para variáveis numéricas e servem principalmente para analisar visualmente a centralidade e dispersão dos dados. No processo de construção do histograma, os dados são categorizados em classes e as frequências são contadas. No eixo horizontal geralmente são mostradas as classes e eixo vertical as frequências que podem ser absolutas ou relativas.
p <- ggplot2::ggplot(base_docentes, aes(x = idade))
p + ggplot2::theme_gray() +
ggplot2::geom_histogram(colour='white', bins = 10) +
ggplot2::labs(y = "Frequência", x = "Faixa de idade",
fill = NULL, title = "") +
ggplot2::scale_x_continuous(
breaks=seq(10, 90, 10),
labels = seq(10, 90, 10)
) +
ggplot2::theme(axis.line = element_blank())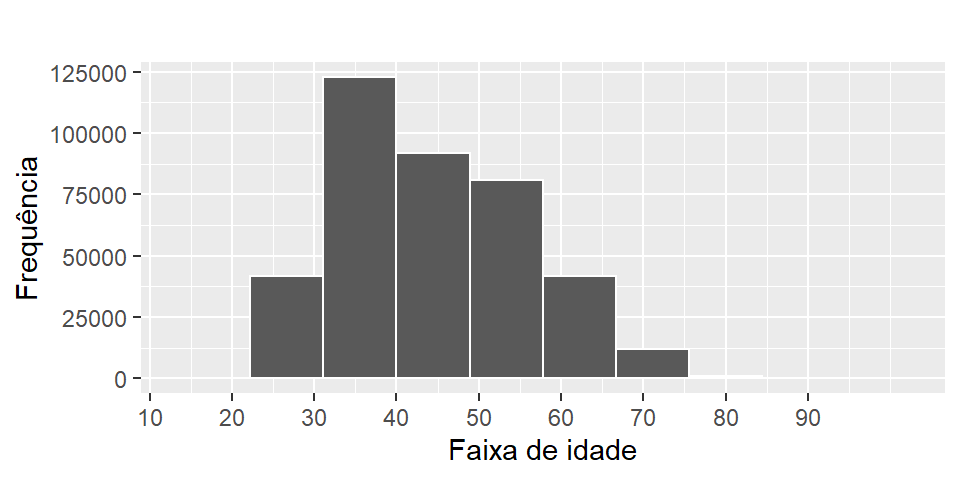
Figura 2.8: Histograma idade do docente
Veja que a figura 2.8 evidencia que as maiores concentrações de docentes estão nas faixas de idade entre 30 e 50 anos.
2.2.4.2 Densidade
Gráficos de densidade possuem aplicação semelhante aos histogramas, porém são mais indicados pata amostras grandes. Ele evidenciam a melhor curva que representam os dados. Este tipo de gráfico nos ajuda também a verificar a distribuição de probabilidade aproximada que os dados podem seguir.
p <- ggplot2::ggplot(base_docentes, aes(x = idade))
p + ggplot2::theme_gray() +
ggplot2::geom_density(adjust = 1) +
ggplot2::labs(y = "Densidade", x = "Idade", fill = NULL, title = "") +
ggplot2::scale_x_continuous(
breaks=seq(10, 90, 10),
labels = seq(10, 90, 10)) +
ggplot2::theme(axis.line = element_blank())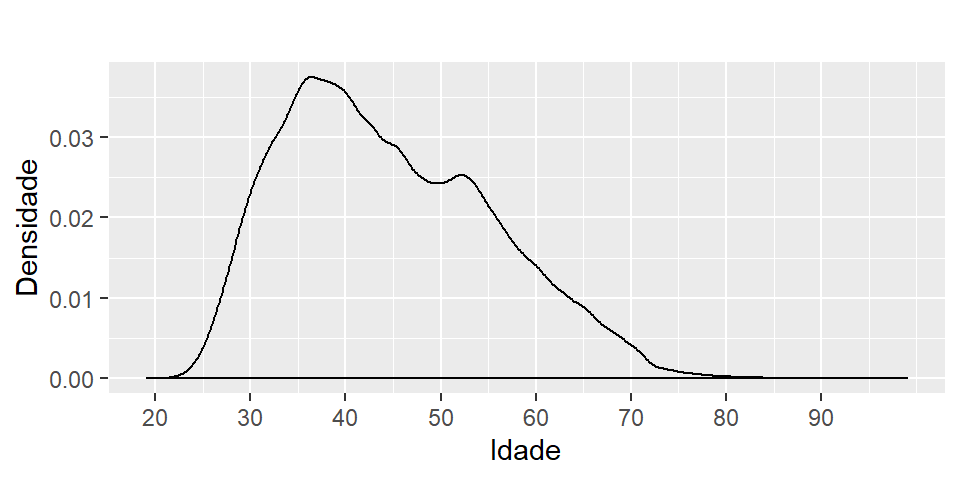
Figura 2.9: Densidade idade do docente
Perceba na figura 2.8 como esperado, que a densidade dos dados está concentrada idade entre 30 e 50 anos. Porém, ela aponta uma elevação próxima a 50 anos apontando comportamento bimodal nos dados.
2.2.4.3 Box-Plot
De longe o gráfico Box-plot ou para muitos, diagrama de caixa é o tipo mais completo de gráfico para variável numérica.
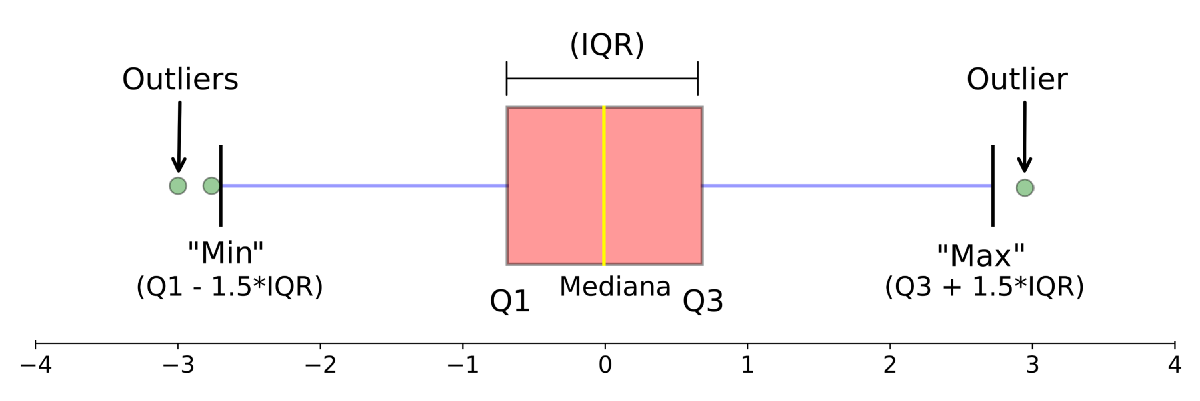
Figura 2.10: Definindo um Box-plot
A figura 2.10 ilustra os elementos que compõem um Box-plot. Perceba que visualmente ele contempla as estatísticas \(Q_1\), \(Q_2\) (mediana), \(Q_3, IQR, LI,LS\) e outliers. Com base nestas estatísticas, uma variável numéricas estará bem caracterizada.
p <- ggplot2::ggplot(base_docentes, aes(y = idade))
p + ggplot2::theme_gray() +
ggplot2::geom_boxplot(adjust = 1) +
ggplot2::labs(x = "", y = "Idade", fill = NULL, title = "") +
ggplot2::coord_flip() +
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())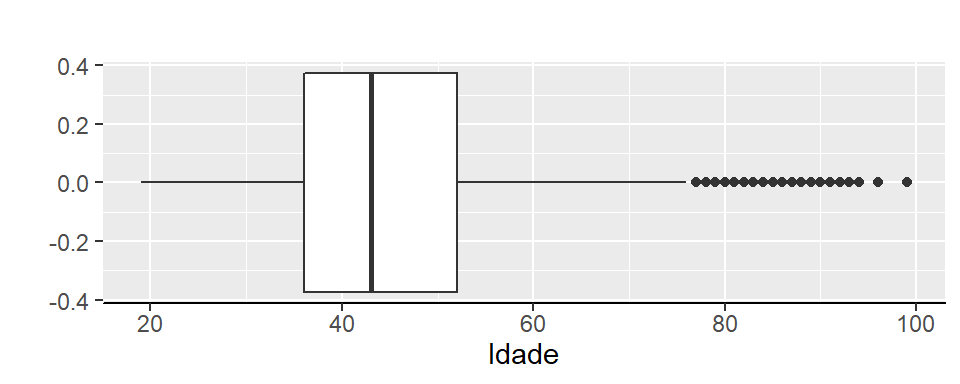
Figura 2.11: Box-plot idade do docente
Conforme vimos antes, idades acima de 76 anos são pontos atípicos na base de docentes, por isso no Box-plot estes pontos aparecem fora do limite superior de outliers na figura 2.20.
2.2.5 Gráficos para duas variáveis numéricas
Os principais gráficos para analisar a relação entre duas variáveis são o gráfico de pontos ou scatterplot e o gráfico de linhas, através deles é possível analisar a relação conjunta entre as variáveis e determinar se uma influencia a outra de alguma forma. além destes, também podemos traçar gráficos de densidade para comparar as duas curvas.
2.2.5.1 scatterplot
O gráfico de pontos é um gráfico bidimensional onde cada eixo representa os valores de uma variável. Este tipo de gráfico é ótimo para analisar a correlação de duas variáveis bem como sua dispersão, pois cada ponto representa a ligação dos elementos das duas variáveis.
p <- base_ies %>%
dplyr::mutate(ReceitaPropria = VL_RECEITA_PROPRIA,
TotalTecnicos = QT_TEC_TOTAL) %>%
dplyr::filter(ReceitaPropria <= 10000000) %>%
ggplot2::ggplot(aes(x = TotalTecnicos, y = ReceitaPropria))
p + ggplot2::theme_gray() +
ggplot2::geom_point() +
ggplot2::labs(x = "Total técnicos", y = "Receita própria",
fill = NULL, title = "") +
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())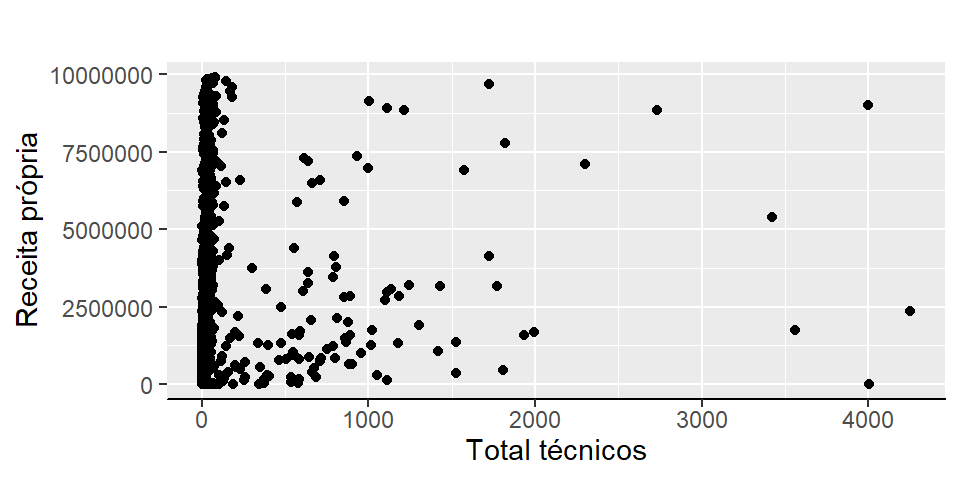
Figura 2.12: Gráfico de pontos total de técnicos versus receita própria
2.2.5.2 Gráfico de linhas
O gráfico de linhas possui aplicação para duas variáveis contínuas e também para séries temporais, onde um dos eixos é uma variável numérica de data.
p <- base_ies %>%
dplyr::mutate(ReceitaPropria = VL_RECEITA_PROPRIA,
TotalTecnicos = QT_TEC_TOTAL) %>%
dplyr::filter(TotalTecnicos < 100) %>%
ggplot2::ggplot(aes(x = TotalTecnicos, y = ReceitaPropria))
p + ggplot2::theme_gray() +
ggplot2::geom_line() +
ggplot2::labs(x = "Total técnicos", y = "Receita própria",
fill = NULL, title = "") +
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())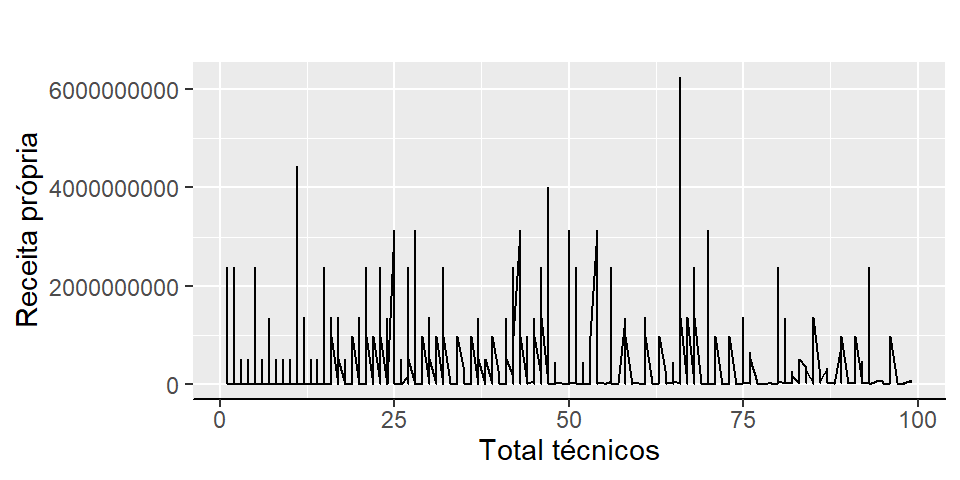
Figura 2.13: Gráfico de pontos total de técnicos (<50) versus receita própria
2.3 Variáveis categóricas versus numéricas
O trabalho estatístico muitas vezes exige que alguma variável numérica seja categorizada ou analisada em conjunto com alguma variável categórica. Todas as técnicas vistas até agora, tanto as medidas estatísticas quanto os gráficos podem ser analisados em conjunto para gerar informação.
2.3.1 Categorizando variáveis numéricas.
Em R podemos agrupar uma variável numérica de muitas formas, umas delas é através das estatísticas de quartis, decis ou percentis dependendo do tamanho da base, com a função quantile() combinada com a função cut(). Outra forma é através do conhecimento próprio do analista com os operadores relacionais do R: <, >, >=, <=, ==, !=, %in% combinadas com ifelse().
## Categorizando por quartis
base_ies <- base_ies %>%
dplyr::mutate(ReceitaPropria = VL_RECEITA_PROPRIA,
TotalTecnicos = QT_TEC_TOTAL)
fx_receita_q <- cut(base_ies$ReceitaPropria,
breaks = round(quantile(base_ies$ReceitaPropria)),
dig.lab = 10, include.lowest = TRUE)
rnp::rnp_freq(fx_receita_q, sortd = FALSE) %>%
knitr::kable(digits = 3,
booktabs = TRUE, format = tb_formata,
caption = "Categorização por quartis") %>%
kableExtra::kable_styling(latex_options = "hold_position")| classe | fa | fr | Faa | Fra |
|---|---|---|---|---|
| 0–1389966 | 612 | 0.25 | 612 | 0.25 |
| 1389966–7429221 | 612 | 0.25 | 1224 | 0.50 |
| 7429221–61258594 | 612 | 0.25 | 1836 | 0.75 |
| 61258594–6248050290 | 612 | 0.25 | 2448 | 1.00 |
## Categorização por ifelse com operadores relacionais
fx_receita_r <- ifelse(base_ies$ReceitaPropria <= 1200000,
"A.-1200000",
ifelse(base_ies$ReceitaPropria <= 5000000,
"B.1200000 a 5000000",
ifelse(base_ies$ReceitaPropria <=35000000,
"C.5000000 a 35000000","D.35000000+")))
rnp::rnp_freq(fx_receita_r, sortd = FALSE) %>%
knitr::kable(digits = 3,
booktabs = TRUE, format = tb_formata,
caption = "Categorização por operadores relacionais") %>%
kableExtra::kable_styling(latex_options = "hold_position")| classe | fa | fr | Faa | Fra |
|---|---|---|---|---|
| A.-1200000 | 571 | 0.233 | 571 | 0.233 |
| B.1200000 a 5000000 | 500 | 0.204 | 1071 | 0.438 |
| C.5000000 a 35000000 | 635 | 0.259 | 1706 | 0.697 |
| D.35000000+ | 742 | 0.303 | 2448 | 1.000 |
No primeiro caso, criamos os cortes utilizando os quartis da variável e em seguida passamos estes cortes para a função cut() que por sua vez particionou a variável de acor com as partes informadas pelo argumento breaks. Desta forma fica mais rápido a categorização, mas o analista não tem como personalizar as faixas. Para atender a esta limitação o segundo método ajuda a customizar as faixas de acordo com a preferência ou necessidade. Embora exija um pouco mais de código, esta última opção é mais flexível.
2.3.2 Medidas estatísticas por agrupamento
Em muitas situações da análise de dados, estamos interessados em analisar a influência de uma variável categórica sob uma ou mais variáveis numéricas. Felizmente, a grande maioria das medidas estatísticas aprendidas até agora se aplicam a este tipo de análise que exige estatísticas agrupadas.
base_docentes %>%
dplyr::group_by(escolaridade) %>%
dplyr::summarise(N = n(),
Min = min(idade),
Q1 = unname(quantile(idade, probs = 0.25)),
Me = mean(idade),
Md = median(idade),
Q3 = unname(quantile(idade, probs = 0.75)),
Max = max(idade)
#Dp = sd(idade),
#cv = sd(idade)/mean(idade)
) %>%
knitr::kable(digits = 2,
booktabs = TRUE, format = tb_formata,
caption = "Estatísticas descritivas idade vs escolaridade") %>%
kableExtra::kable_styling(latex_options = "hold_position")| escolaridade | N | Min | Q1 | Me | Md | Q3 | Max |
|---|---|---|---|---|---|---|---|
| 1. Sem graduação | 10 | 23 | 47.25 | 52.60 | 54 | 63 | 66 |
| 2. Graduação | 4613 | 20 | 27.00 | 37.78 | 33 | 45 | 94 |
| 3. Especialização | 72301 | 19 | 35.00 | 43.01 | 41 | 50 | 93 |
| 4. Mestrado | 154285 | 22 | 34.00 | 42.81 | 41 | 50 | 90 |
| 5. Doutorado | 160827 | 19 | 38.00 | 47.06 | 46 | 54 | 99 |
Em \(Q3\) temos que 75% dos docentes com Doutorado possuem idade até 54 anos. Vemos também alguns doutores excepcionais com idade mínima de 19 anos. A idade máxima registrada foi de 99 anos presente no grupos dos doutores. A categoria sem graduação tem dez indivíduos e é pouco representativa.
2.3.3 Gráficos para categóricas vs numéricas
Com apoio do pacote ggplot podemos combinar a maioria dos gráficos vistos até agora para analisar dados por grupo ou classes. Como citamos na seção 1.6 uma das ferramentas estatísticas é a análise bivariada e ela pode ser feita entre duas variáveis podendo ser de mesmo tipo ou de tipos diferentes
- Box-plot agrupado: Box-plots por categoria são muito informativos uma vez que resumem sete estatísticas fundamentais de uma variável continua conforma já vimos.
p <- base_docentes %>%
ggplot2::ggplot(aes(x = escolaridade, y = idade, fill = escolaridade))
p + ggplot2::theme_gray() +
ggplot2::geom_boxplot(show.legend = FALSE) +
ggplot2::coord_flip()+
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())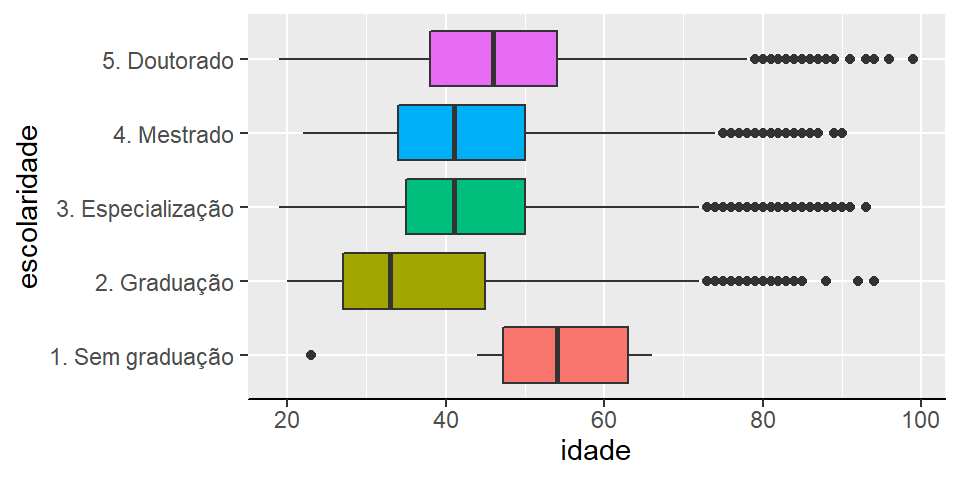
Figura 2.14: Box-plot de idade vs escolaridade
No Box-plot conseguimos ver que docentes com graduação apenas são minoria como visto na tabela e doutores são maioria. Notamos também que, com exceção daqueles sem graduação todos os grupos possuem dispersão parecida uma vez que a distância entre \(Q_1\) e \(Q_3\) é pequena.
Para todos os gráficos agrupados também é possível quebrar a visualização em um gráfico por categoria adicionando uma terceira variável com facet_wrap() .
p <- base_docentes %>%
ggplot2::ggplot(aes(x = sexo, y = idade, fill = escolaridade))
p + ggplot2::theme_gray() +
ggplot2::geom_boxplot(show.legend = FALSE) +
ggplot2::coord_flip()+
ggplot2::facet_wrap(escolaridade~.)+
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())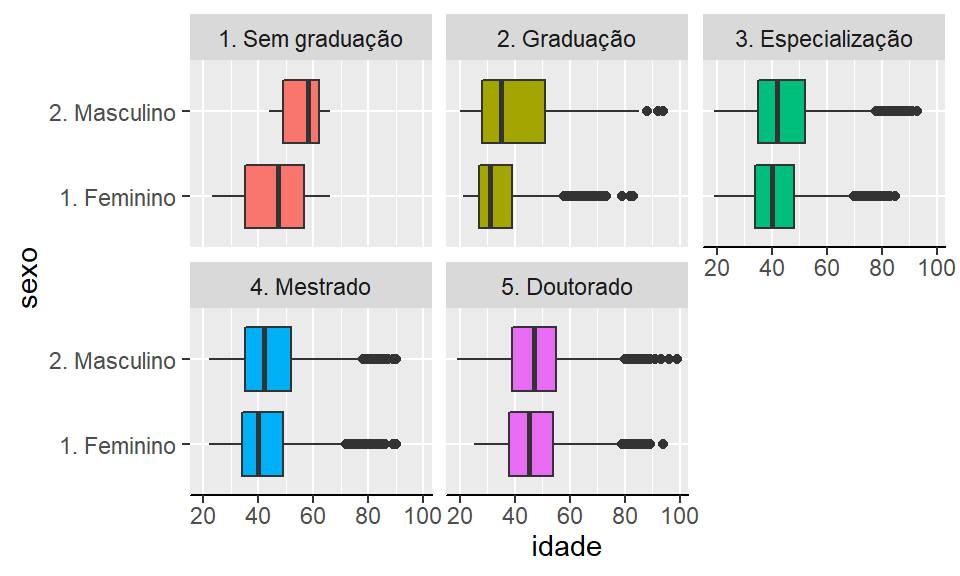
Figura 2.15: Box-plot de idade vs escolaridade por sexo
- Gráfico de densidade agrupado: é possível comparara várias curvas simultaneamente no mesmo gráfico para analisar a distribuição dos dados.
p <- base_docentes %>%
ggplot2::ggplot(aes(x = idade, fill = escolaridade))
p + ggplot2::theme_gray() +
ggplot2::geom_density(alpha = 0.6) +
ggplot2::theme(legend.position = "right") +
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL, axis.line.y = element_blank()) +
ggplot2::labs(x = "Idade", y = "Densidade", fill = NULL, title = "")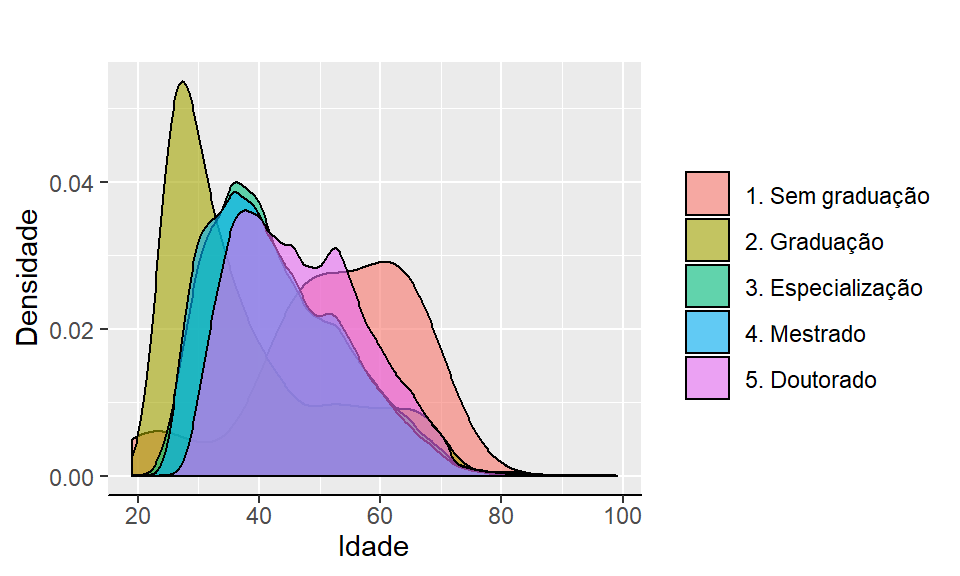
Figura 2.16: Densidade de idade vs escolaridade
O resultado é um gráfico elegante e que indica precisamente a forma da distribuição dos dados.
Agora quebrado por sexo.
p <- base_docentes %>%
ggplot2::ggplot(aes(x = idade, color = sexo, fill = escolaridade))
p + ggplot2::theme_gray() +
ggplot2::geom_density(alpha = 0.6, show.legend = FALSE) +
ggplot2::facet_wrap(~escolaridade)+
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank()) +
ggplot2::labs(x = "Idade", y = "Densidade", fill = NULL, title = "")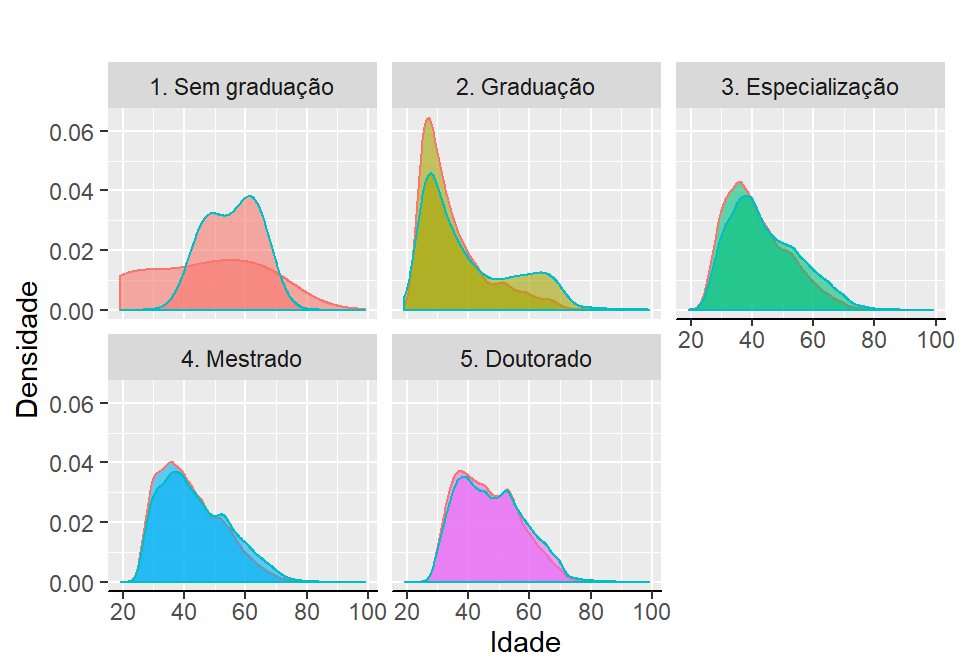
Figura 2.17: Densidade de idade vs escolaridade por sexo
- Gráfico de colunas agrupadas: é possível assim, como nos dois últimos exemplos, gerar gráficos e coluna agrupadas e fazer a quebra adicionando uma terceira variável.
p <- base_docentes %>%
ggplot2::ggplot(aes(x = escolaridade, y = idade, fill = sexo))
p + ggplot2::theme_gray() +
ggplot2::geom_col(show.legend = TRUE, position = "dodge") +
ggplot2::theme(legend.position = "bottom") +
ggplot2::coord_flip()+
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())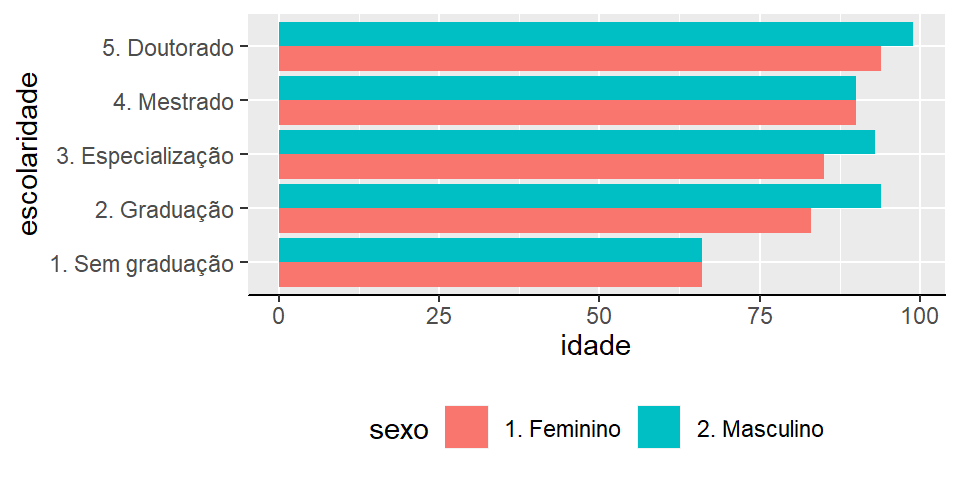
Figura 2.18: Colunas de idade vs escolaridade por sexo
- Histogramas agrupados: Histogramas também são agrupáveis segundo as categorias da variável.
p <- base_docentes %>%
ggplot2::ggplot(aes(x = idade, fill = escolaridade))
p + ggplot2::theme_gray() +
ggplot2::geom_histogram(bins = 10, show.legend = FALSE) +
ggplot2::facet_wrap(.~escolaridade)+
ggplot2::theme(axis.line.x = element_line(),
axis.text.x = NULL,
axis.line.y = element_blank())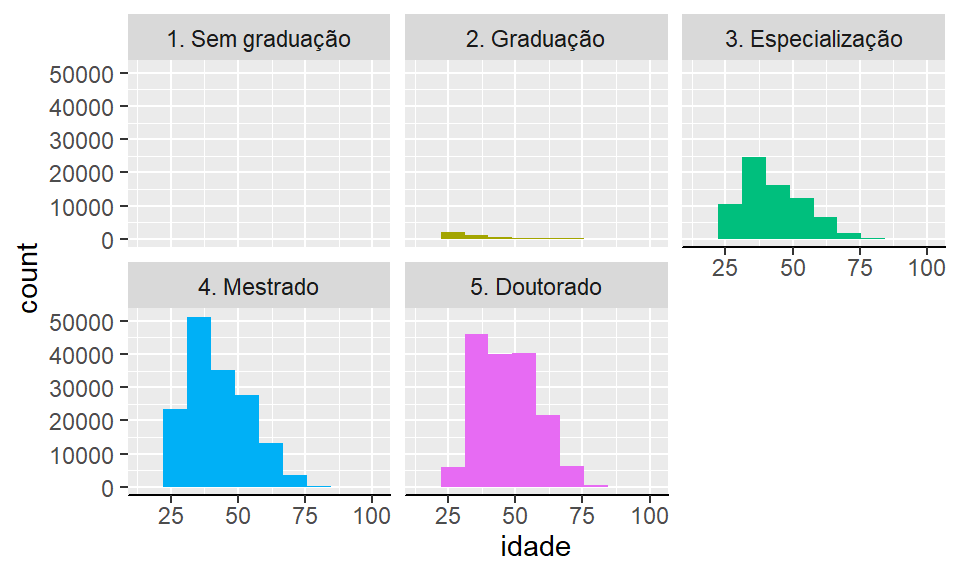
Figura 2.19: Histograma de idade vs escolaridade
2.4 Medidas de associação e correlação
Análises univariadas são muito úteis para determinarmos particularidades de dados porém, em muitas situações, desejamos medir relações de interdependência entre duas ou mais variáveis. Como vimos em gráficos para duas variáveis numérias; gráficos para duas variáveis categóricas e também em tabelas de contingência, é possível extrair características importantes dos valores e/ou das classes de cada variável de várias formas. Contudo, queremos quantificar a relação global de duas ou mais variáveis e neste sentido, as medidas de associação e de correlação tem papel fundamental. Suponha que desejamos determinar de a variável idade dos docentes está associada à escolaridade ou se o total de técnicos está correlacionado com a receita total das IES. Trataremos nesta sessão algumas medidas de associação entre duas variáveis categóricas onde trabalharemos com as estatísticas \(\chi^2\) (Qui-quadrado), \(V\) de Cramer, \(C\) coeficiente de contingência. Para as variáveis numéricas trabalharemos com as estatísticas de correlação \(\rho\) de Pearson e Coeficiente de correlação rank de Spearman que são medidas mais recorrentes em aplicações práticas.
2.4.1 Associação entre duas variáveis discretas
Duas variáveis discretas são ditas independentes ou não associadas quando as observações de uma não influenciam as observações da outra. Por exemplo, quando duas pessoas jogam uma moeda separadamente dez vezes, o resultados da primeira pessoa não são afetados pelos resultados da segunda pessoa.
2.4.1.1 Estatística \(\chi^2\)
A estatística \(\chi^2\) é muito utilizada para quantificar a associação global de duas variáveis categóricas dispostas em uma tabela de contingência com \(k \times l\) linhas vs colunas. Esta estatísticas é dada por:
\[\chi^2 = \sum_{i=1}^{k} \sum_{j=1}^{l} \frac{(n_{ij} - \widetilde{n}_{ij})^2}{\widetilde{n}_{ij}}\]
onde \(\widetilde{n}_{ij}\) é a frequência esperada de \((x_i;y_j)\) dada pelo produto das frequências absolutas marginais e calculado por
\[\widetilde{n}_{ij} = \frac{n_{i+}\times n_{+j}}{n}\]
Para que a estatística seja confiável, os seguintes pressupostos devem ser respeitados:
- A amostra deve ser aleatória;
- Todas as frequências esperadas são maiores ou iguais a 1;
- Não mais de 20% das frequências esperadas são inferiores a 5;
Caso os desvios entre as frequências observadas e esperadas seja alto temos evidência de associação forte porque as frequências relativas esperadas são calculadas assumindo independência entre as duas variáveis. Desta forma, se o posto ocorrer, ou seja, se as frequências relativas observadas e esperadas são idênticas ou similares a associação é fraca e as variáveis são independentes. O range da estatística está limitado a
\[0 \le \chi^2 \le n\times(min(k,l)-1)\]
Assim, uma forma de verificar a força da associação é comparar o valor de \(\chi^2\) calculado com o valor máximo que \(\chi^2\) pode assumir, ou seja \(n\times(min(k,l)-1)\) onde \(n\) é o total geral. Esta métrica depende unicamente do tamanho da amostra e total de classes de cada variável da tabela de contingência.
É provado que a estatística \(\chi^2\) segue uma distribuição qui-quadrado com \(\nu\) graus de liberdade calculados com base no total de classes das variáveis da tabela de contingência \(\nu = (k-1)\times (l-1)\). Veremos em testes de hipóteses como quantificar a incerteza do teste de \(\chi^2\) através do p-valor do teste. Por hora, apresentamos apenas a estatística geral.
\(f_{11} = 10 \times 179856 / 392036 = 4.6\)
\(f_{12} = 10 \times 212180 / 392036 = 5.4\)
\(f_{21} = 4613 \times 179856 / 392036 = 2116.0\)
\(f_{22} = 4613 \times 212180 / 392036 = 2497.0\)
\(f_{31} = 33169.8\)
\(f_{32} = 39131.2\)
\(f_{41} = 70782.0\)
\(f_{42} = 83503.0\)
\(f_{51} = 73783.3\)
\(f_{52} = 87043.7\)
\(\chi^2 = \frac{(3-4.6)^2}{4.6} + \frac{(7-5.4)^2}{5.4}+...+\frac{(87015-87043.7)^2}{87043.7} = 655.0\)
Agora calculamos o valor máximo que \(\chi^2\) pode assumir \(392036 \times (min(i=5,j=2)-1) = 392036\). Como \(655.0\) está muito longe de \(392036\) podemos afirmar que não existe associação forte entre escolaridade e sexo dos docentes, ou seja estas duas variáveis são independentes.
Em R podemos calcular a estatística e as frequências esperadas através da função chisq.test() em conjunto com a função table().
chisq.test()
# Sem utilizar a chisq.test()
observado <- table(base_docentes$escolaridade, base_docentes$sexo)
observado##
## 1. Feminino 2. Masculino
## 1. Sem graduação 3 7
## 2. Graduação 1848 2765
## 3. Especialização 30579 41722
## 4. Mestrado 73614 80671
## 5. Doutorado 73812 87015## 1. Feminino 2. Masculino
## 1. Sem graduação 4.588 5.412
## 2. Graduação 2116.325 2496.675
## 3. Especialização 33169.833 39131.167
## 4. Mestrado 70781.977 83503.023
## 5. Doutorado 73783.277 87043.723## [1] 647.2##
## 1. Feminino 2. Masculino
## 1. Sem graduação 4.588 5.412
## 2. Graduação 2116.325 2496.675
## 3. Especialização 33169.833 39131.167
## 4. Mestrado 70781.977 83503.023
## 5. Doutorado 73783.277 87043.723## X-squared
## 647.2## [1] 3920362.4.1.2 Estatística \(V\) de Cramér
Estatística \(\chi^2\) possui uma fragilidade que pode dificultar a interpretação, pois ela depende do range e este por sua vez depende do tamanho da amostra e da quantidade de classes em cada variável. A esteatítica \(V\) surge como uma forma de padronização da estatística \(\chi^2\) e é calculada por:
\[V = \sqrt{\frac{\chi^2}{n \times (min(k,l)-1)}}\]
Esta estatística torna a interpretação de \(\chi^2\) mais simples, pois seu retorno é um número menor ou igual a uma unidade e quanto mais próximo de um, mais forte será a associação entre as duas variáveis.
Tabelas de interpretação de estatísticas de associação como \(V\) são questionáveis uma vez que o nível de associação pode variar de acordo com tipo de estudo, área de pesquisa ou até preferência do pesquisador. Porém, algumas autores se guiam pelas faixas da tabela 2.12 para interpretar o nível da associação entre duas variáveis numa tabela de contingência. Estes valores são adaptados de (Gravetter and Wallnau 2016).
| Faixa | Interprecao |
|---|---|
| 0.00–0.10 | muito fraca |
| 0.10–0.30 | fraca |
| 0.30–0.50 | moderada |
| 0.5 > | forte |
\[V = \sqrt{\frac{647.2}{392036 \times (min(5,2)-1)}} = \sqrt{\frac{647.2}{392036 \times (2-1)}} = 0.0406\]
Como \(V = 0.0406 < 0.10\) concluímos que não existe associação estatisticamente significativa entre escolaridade e sexo.
dm_curso possui as variáveis DESC_IN_MATERIAL_BRAILLE e DESC_IN_MATERIAL_TATIL que se referem a recursos extras disponibilizados para os cursos. Verifique se estas variáveis estão associadas através das estatísticas \(\chi^2\) e \(V\)
data(dm_curso, package = "rnp")
# Tabela de contingência
observado <- table(dm_curso$DESC_IN_MATERIAL_BRAILLE,
dm_curso$DESC_IN_MATERIAL_TATIL)
# Com a chisq.test()
t1 <- chisq.test(observado)
# Estatística e Range
t1$statistic## X-squared
## 52186## [1] 71386Vamos calcular a estatística \(V\)
\[V = \sqrt{\frac{52186}{ 35693 \times (min(3,3)-1)}} = \sqrt{\frac{52186}{35693 \times (3-1)}} = 0.8550\]
Como \(V\) está muito acima de 0.50 logo, temos evidẽncias de que estas duas variáveis são fortemente associadas.
Perceba que o próprio nome de cada variável contém um indicativo de associação uma vez que espera-se que materiais para aulas em braile devam conter itens de táteis. Aqui o analista entra com o senso de negócio para confirmar se as estatísticas fazem sentido prático na validação das hipóteses de pesquisa.
2.4.1.3 Estatística \(C\) coeficiente de contingência
O coeficiente de contingência é outra medida de associação que depende da estatística \(\chi^ 2\) e foi pensada para ser uma versão corrigida da estatística \(\chi^2\). Os valor de \(C\), assim como os de \(V\) estão no intervalo \([0,1]\) e quanto maior mais forte será a associação entre as duas variáveis na tabela de contingência.
\[C = \sqrt{\frac{min(k,l)}{min(k,l)-1}} \times \sqrt{\frac{\chi^2}{\chi^2 + n}} \]
Estas três estatísticas de associação podem ser calculadas pela função rnp::rnp_associacao() no nosso pacote ou através da função vcd::assocstats() do pacote vcd.
rnp::rnp_associacao() temos que:
data(dm_curso, package = "rnp")
rnp::rnp_associacao(x = dm_curso$DESC_IN_MATERIAL_BRAILLE,
y = dm_curso$DESC_IN_MATERIAL_TATIL)## Qui-quadrado V-Cramer C-Contingencia
## 52185.5662 0.8550 0.94382.4.2 Duas ou mais variáveis numéricas
Na análise bivariada ou multivariada de variáveis numéricas, a covariância e a correlação tem papel fundamental. Ambas se assemelham pelo fato de que medem a direção da relação entre duas variáveis ao longo de seus pontos. As relações mais comuns são ambas as variáveis crescem, ambas decrescem, uma decresce e a outra cresce. A diferença mais significativa entre a covariância e a correlação é que a primeira oferece um valor absoluto variando de acordo com os dados, graças a isso não tem como estimar a força de uma relação linear. É aí que entra a correlação. Em R a covariância pode ser calculada por var() e cov() e a correção por cor() e se aplica a bases com mais de 2 variáveis numéricas.
2.4.2.1 Covariância
O conceito de covariância pode ser aplicado tanto a conjunto de dados como a variáveis aleatórias. Quando aplicada a duas variáveis \(X\) e \(Y\) é expressa por:
\[Cov(X,Y) = \frac {\sum_{i=1}^N(X_i-\bar X)(Y_i - \bar Y)}{N-1}, i=1,..,N\]
Sendo que \(\bar X\) e \(\bar Y\) são as médias das variáveis X e Y.
TotalTecnicos e ReceitaProprianos dados das IES
base_ies %>%
dplyr::select(TotalTecnicos, ReceitaPropria) %>%
cov() %>%
knitr::kable(booktabs = TRUE, format = tb_formata,
caption = "Análise de covariância") %>%
kableExtra::kable_styling(latex_options = "hold_position")| TotalTecnicos | ReceitaPropria | |
|---|---|---|
| TotalTecnicos | 341089 | 14066046853 |
| ReceitaPropria | 14066046853 | 173738053485884832 |
Note que os números são extremamente grandes e tudo que podemos tirar é que a covariância é positiva entre as duas variáveis, mas não conseguimos estimar a força desta relação.
Os elementos da diagonal principal da matriz de covariâncias representam a variância de cada variável e os valores fora da diagonal são covariâncias. A matriz é espelhada e para interpretá-la basta ler acima ou abaixo da diagonal principal.
2.4.2.2 Correlação de Pearson
A correlação linear ou de Pearson é uma estatística padronizada que varia de \(-1\) a \(1\) e expressa a relação linear entre duas variáveis numéricas. A correlação é expressa pela letra grega \(\rho\) e é dada pela seguinte expressão matemática:
\[\rho = \frac {\sum_{i=1}^N(X_i-\bar X)(Y_i - \bar Y)}{\sqrt{\sum_{i=1}^N(X_i-\bar X)^2} \times \sqrt{\sum_{i=1}^N(Y_i-\bar Y)^2}}=\frac{Cov(X,Y)}{\sqrt{S^2(X) \times S^2(Y)}}, \\ i=1,..,N\]
Em resumo, esta formula aparentemente complicada diz que a correlação é resultado da covariância dividida pela raiz quadrada do produto das variâncias de cada variável.
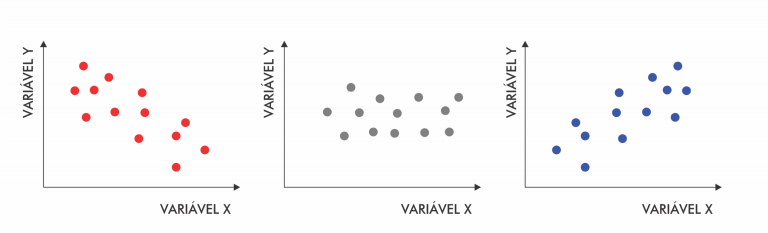
Figura 2.20: Tendência da correlação
A figura 2.20 ilustra a relação entre duas variáveis \(X\) e \(Y\). Da esquerda para a direita temos correlação linear negativa forte (tende a \(-1\)), correlação fraca (tende a \(0\)) e correlação linear positiva forte (tende a \(+1\)).
Como regra geral, costuma-se considerar a distribuição expressa na tabela 2.14 para interpretar a correlação. A mesma se aplica para negativa ou positiva bastando apenas dizer estar alerta ao sinal de \(\rho\).
| Faixa | Interprecao |
|---|---|
| 0.00–0.19 | muito fraca |
| 0.20–0.39 | fraca |
| 0.40–0.69 | moderada |
| 0.70–0.89 | forte |
| 0.90–1.00 | muito forte |
DespesaPesquisa.
base_ies %>%
dplyr::transmute(TotalTecnicos = QT_TEC_TOTAL,
ReceitaPropria = VL_RECEITA_PROPRIA,
DespesaPesquisa = VL_DESPESA_PESQUISA) %>%
cor(method = "pearson") %>%
round(digits = 3) %>%
knitr::kable(booktabs = TRUE, format = tb_formata,
caption = "Análise de correlação") %>%
kableExtra::kable_styling(latex_options = "hold_position")| TotalTecnicos | ReceitaPropria | DespesaPesquisa | |
|---|---|---|---|
| TotalTecnicos | 1.000 | 0.058 | 0.292 |
| ReceitaPropria | 0.058 | 1.000 | 0.064 |
| DespesaPesquisa | 0.292 | 0.064 | 1.000 |
Note agora que faz mais sentido estimar a força da relação linear entre as variáveis utilizando a correlação. No nosso exemplo, uma correlação linear de 0.047 entre TotalTecnicos e ReceitaPropria nos diz que a relação linear entre estas duas variáveis é muito fraca. O mesmo se aplica à variável DespesaPesquisa em relação à variável TotalTecnicos com 0.190. Estas três variáveis não possuem correlação forte entre si.
2.4.2.3 Correlação rank de Spearman
Para ilustrar esta correlação, vamos imaginar que dois jurados avaliem a qualidade do ensino em cada uma das IES mapeadas no censo, por algum método de forma independente e atribuam uma nota numérica de 0 a 100 onde notas baixas sejam ruins e altas sejam boas. Vamos chamar esta nota de escore e definir por \(x_i\). Ao ordenarmos todas as IES pelas notas das maiores para as menores teremos um rank que vai de 1 para o primeiro lugar até o total de IES (assumindo que não há empates). Ao selecionarmos uma IES qualquer do conjunto de dados, teremos dois ranks, \(R(x_i)\) e \(R(y_i)\) para ela e consequentemente uma diferença entre os ranks dada por \(d_i = R(x_i) - R(y_i)\). Por exemplo, se a UFPR teve os ranks 20 e 25, temos que \(d_i = 20-25 = 5\). O coeficiente de correlação rank de Spearman busca medir a força da associação entre os dois julgamentos dos dois jurados. Calculamos o coeficiente de correlação rank de Spearman por
\[ R = 1 - \frac{6 \times \sum_{i = 1}^{n} d^2_i}{n \times (n^2 - 1)}\] Este tipo de correlação se aplica para variáveis contínuas e também ordinais e conforme já exposto, busca medir a correlação através dos ranks de cada variável e varia de \(-1\) a \(+1\). Quando \(R=+1\) temos que as duas variáveis foram rankeadas exatamente iguais (concordância ou associação perfeita) e \(R=-1\) quando ocorreu o oposto (não concordância).
TotalTecnicos e ReceitaPropria para as 10 primeiaras observações da base de dados dm_ies.
temp <- base_ies %>%
head(n = 10) %>%
dplyr::transmute(TotalTecnicos = QT_TEC_TOTAL,
`R(xi)` = rank(-TotalTecnicos),
ReceitaPropria = VL_RECEITA_PROPRIA,
`R(yi)` = rank(-ReceitaPropria),
di = `R(xi)`-`R(yi)`,
di2 = di^2)
# Tabela de exemplo
knitr::kable(x = temp, booktabs = TRUE, format = tb_formata,
caption = "Análise de correlação de Spearman") %>%
kableExtra::kable_styling(latex_options = "hold_position")| TotalTecnicos | R(xi) | ReceitaPropria | R(yi) | di | di2 |
|---|---|---|---|---|---|
| 1574 | 3 | 6913132 | 7 | -4 | 16 |
| 3206 | 1 | 63239902 | 6 | -5 | 25 |
| 1429 | 4 | 3161937 | 10 | -6 | 36 |
| 1721 | 2 | 4136205 | 8 | -6 | 36 |
| 786 | 8 | 3458763 | 9 | -1 | 1 |
| 1275 | 5 | 616991005 | 1 | 4 | 16 |
| 441 | 9 | 142785305 | 4 | 5 | 25 |
| 986 | 7 | 338035351 | 3 | 4 | 16 |
| 1062 | 6 | 487902230 | 2 | 4 | 16 |
| 246 | 10 | 100089191 | 5 | 5 | 25 |
## [1] -0.2848## [1] -0.2848Concluímos que, via correlação de Spearman, temos associação negativa baixa entre total de técnicos e total de receita própria. Como vimos, o coeficiente de correlação é determinado pela função cor() padrão do R e ela cobre três tipos de coeficientes. Especialmente para o R NA PRÁTICA, criamos a função rnp_correlacao() que determina a correlação de Pearson, Spearman e Kendal. Esta última não abordaremos aqui, mas ela também é indicada para variáveis ordinais porém focada em pares concordantes versus discordantes. para os leitores interessados sugerimos (Kendall 1938).
temp <- base_ies %>%
dplyr::transmute(TotalTecnicos = QT_TEC_TOTAL,
ReceitaPropria = VL_RECEITA_PROPRIA,
DespesaPesquisa = VL_DESPESA_PESQUISA)
rnp::rnp_correlacao(temp) %>%
knitr::kable(booktabs = TRUE, format = tb_formata, row.names = FALSE,
caption = "Correlação com rnp_correlacao()") %>%
kableExtra::kable_styling(latex_options = "hold_position")| x | y | pearson | spearman | kendall |
|---|---|---|---|---|
| TotalTecnicos | DespesaPesquisa | 0.2918 | 0.3724 | 0.2827 |
| TotalTecnicos | ReceitaPropria | 0.0578 | 0.5253 | 0.3963 |
| ReceitaPropria | DespesaPesquisa | 0.0642 | 0.1957 | 0.1583 |
2.5 Exercícios de estatística descritiva
Objetivo: Fazer uma análise descritiva dos dados do censo da educação superior de 2017. Neste questionário, o analista será testado em uma situação real onde os conhecimentos práticos de estatística descritiva e R serão postos à prova.
Instruções: Utilize tabelas, gráficos e tudo que aprendeu nos dois capítulos de estatística descritiva bem como revise os exemplos em R. Se preferir pode baixar os dados direto do site do INEP e em caso de dúvidas sobre as variáveis, consulte o dicionário de dados que vem junto dos dados baixados. Lembrando, temos os dados já prontos no pacote
rnp, bastando apenas fazer o carregamento.- Dados rnp::dm_ies - Estes são dados das Instituições de Ensino Superior do brasil;
- Dados rnp::dm_curso - Dados sobre os cursos de nível superior das IES;
- Dados rnp::dm_docente - Dados dos docentes de ensino superior;
Se for baixar os dados do INEP veja a ajuda das funções
rnp::rnp_get_inep_censo()ernp::rnp_get_classes_inep()para ver como baixar os dados e aplicar a descrição das categorias das variáveis.
Exercício 2.13 Verifique as três bases de dados e explore:
- Verifique a estrutura dos dados;
- Quantas variáveis e observações cada uma tem?
- Quais os tipos de dados cada uma tem (character, fator, etc.)?
- Quais os tipos de variáveis (numérica, categórica, etc.)?
Exercício 2.14 Analisar informações relevantes sobre as instituições de ensino superior focando nas seguintes perguntas:
- Qual a distribuição de frequências das IES por categoria administrativa e por organização acadêmica?
- Qual a distribuição das IES por estado e região;
- Qual a quantidade de funcionários técnico-administrativos por estado e por região;
- Qual o volume de receita e de despesas total das IES no período por estado?
- Quais os top 10 estados com maior percentual de saldo (dinheiro que sobra depois de pagar as despesas em relação ao total de receita)?
- Quais os top 10 estados que possuem maior investimento em pesquisa nas suas IES?
- Faça um resumo descritivo das variáveis de receita e despesas e verifique pontos atípicos;
- Existe correlação entre as receitas e despesas das IES?
- Represente por Box-plot a receita das IES por UF e por região. Quais merecem atenção?
Exercício 2.15 Analisar informações relevantes sobre os cursos superiores.
- Quais os top 10 cursos com mais vagas no Brasil?
- Quais os top 10 cursos com maiores taxas de conclusão em relação ao total de vagas?
- Analise o número de vagas, ingressos, matrículas e concluintes por UF utilizando o resumo dos cinco números?
- Qual a taxa média de conclusão por UF onde existe a oferta?
- Verifique a correlação entre no total de vagas e total de ingressos.
- Utilize a estatística \(V\) de Cramér e o coeficiente de contingência para verificar se existe associação entre as variáveis categoria administrativa, grau acadêmico e organização escolar duas a duas.
Exercício 2.16 Obter informações relevantes sobre os docentes.
- Qual a distribuição de docentes por Categoria Administrativa e por escolaridade?
- E por regime de trabalho e sexo?
- Qual a idade média dos docentes por sexo e escolaridade? Mostre através de Box-plots ou histogramas.
- Verifique se existe associação entre categoria administrativa e raça ou entre raça e escolaridade
Referências
Barnett, Vic, and Toby Lewis. 1974. Outliers in Statistical Data. Wiley.
Gravetter, Frederick J, and Larry B Wallnau. 2016. Statistics for the Behavioral Sciences. Cengage Learning.
Kendall, Maurice G. 1938. “A New Measure of Rank Correlation.” Biometrika 30 (1/2): 81–93.
Komsta, Lukasz. 2011. Outliers: Tests for Outliers. https://CRAN.R-project.org/package=outliers.
Reichmann, WJ. 1961. “Use and Abuse of Statistics: Methuen.” 1961.
Tufte, Edward, and P Graves-Morris. 2014. “The Visual Display of Quantitative Information.; 1983.”