Capítulo - 1 Estatística
A Estatística é um ciência vasta e para tentar entender melhor do que ela trata, vamos conferir algumas definições formais e outras não tão formais.
1.1 O que é estatística?
Segundo o dicionário Aurélio, a estatística é:
“Ramo das matemáticas aplicadas cujos princípios decorrem da teoria das probabilidades e que tem por objeto o estudo, bem como o agrupamento metódico, de séries de fatos ou de dados numéricos. — Dicionário Aurélio”

Figura 1.1: Tenho uma dúvida
Calma meu jovem. De fato esta definição é muito complicada. Vamos ver outras definições então!
O dicionário do Google também define como:
Ramo da matemática que trata da coleta, da análise, da interpretação e da apresentação de massas de dados numéricos. — Google
A definição do Google está incompleta, pois não considera dados em formato de texto, apenas numéricos. Temos mais algumas frases a seguir!
A estatística é a arte de nunca ter que dizer que você está errado. — C. J. Bradfield
Aqui temos uma brincadeira do meio estatístico que expressa flexibilidade. É possível, porém não recomendado contar meias verdades com estatística.
Temos ainda a minha favorita!
Estatística é a arte de torturar os números até que eles confessem. — Desconhecido
Esta brincadeira aparentemente inocente guarda um fato interessante: se explorarmos e estressarmos os dados ao extremo, sempre teremos alguma resposta. Nem sempre é o que queremos saber ou concluir, mas com certeza tiraremos alguma informação dos mesmos utilizando técnicas estatísticas adequadas.

Figura 1.2: Não tenho mais dúvidas
Diante das definições acima, uma boa adaptação em português mais simples seria:
A Estatística é a ciência baseada em probabilidade que fornece métodos para a coleta, organização, descrição , apresentação, análise e interpretação de dados para suportar a tomada de decisão. — Adaptação
Com base nas definições citadas, fica claro que a estatística serve como uma ciência de apoio à tomada de decisão através de dados. Um jargão que vem sendo utilizado cada vez mais em Analytics, especialmente no marketing é data-driven. Uma empresa que diz possuir uma data-driven culture deverá ter sua cultura a tomada e decisão com base nos dados. Para isso ocorrer de forma excelente, a estatística estará em todas as frentes garantindo precisão, qualidade e confiabilidade nos números que apoiarão a tomada de decisão. Isso faz com que esta ciência seja de total relevância para todos que querem descobrir e entender o que seus dados estão tentando esconder para que seus negócios funcionem de forma otimizada.
O processo de coleta, organização, descrição dos dados, cálculo e interpretação de estatísticas pertencem à Estatística descritiva, enquanto a análise e a interpretação dos dados, associado a uma margem de incerteza, geralmente associada a uma amostra ficam por conta da Estatística inferencial ou indutiva fortemente fundamentada na teoria das probabilidades que veremos em módulo específico.
1.2 Fases do trabalho estatístico
No contexto das empresas, em geral o planejamento estatístico não existe ou não é feito de forma consistente e isso ocorre muitas vezes devido ao fato de as companhias geram dados de acordo com seus próprios produtos e processos e muitas vezes sem se dar conta de que os dados poderão gerar valor. Em muitos casos, o acúmulo desordenado de dados dificulta a obtenção de conhecimento e consequente tomada de decisão. Empresas competitivas entendem o valor dos dados e investem esforço, tempo e dinheiro para gerar bases de dados robustas e orientadas para o trabalho de Data Science. Por isso, sempre que possível devemos nos esforçar para inserir o trabalho estatístico no planejamento de processos seguindo recomendações científicas, pois isso garantirá que as melhores ferramentas e técnicas serão empregadas desde o início da geração dos dados e maximizará o valor esperado.
Como planejar pesquisas estatísticas e experimentos são temas profundos e que não cobriremos neste texto, mas para os leitores interessados sugerimos os textos de (Gil 2008) para Métodos e Técnicas de Pesquisa; Fundamentos de metodologia científica do (Köche 2016). Para planejamento de experimentos, sugerimos o texto de (Montgomery 2017).
A figura 1.3 exibe um roadmap das principais etapas do processo estatístico.
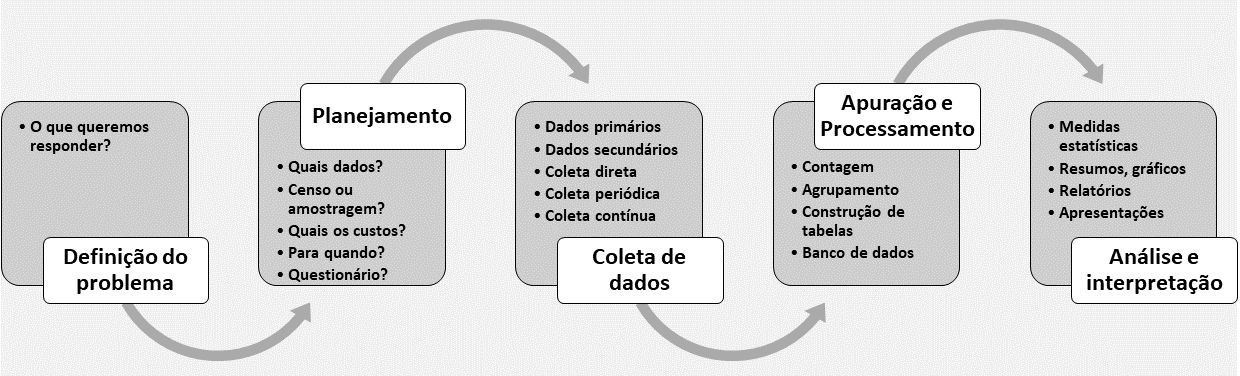
Figura 1.3: Fases do trabalho estatístico
Definição do problema: Este processo inicia sempre pela Definição do problema. Nesta fase inicial é preciso delimitar muito bem o problema de pesquisa. Seja ele simples ou complexo, se esta etapa for mal pensada, poderá conduzir a resultados inesperados ou questões não respondidas;
Planejamento: Nesta etapa é preciso responder muitos porquês, afinal não podem restar dúvidas que comprometam futuramente os trabalhos. Deve-se responder questões sobre quais dados utilizar, tamanho e tipo das amostras, custos do projeto, tempo de execução, ferramentas, pessoal qualificado e uma série de questões relacionadas ao projeto.
Coleta dos dados: Na etapa de coleta, o pesquisador deve estar atento ás fontes de dados e à qualidade dos mesmos. Seja através de questionários ou de bases já montadas, os dados precisam ser confiáveis e consistentes. Os dados devem ser catalogados respeitando-se o tipo de coleta, se periódica, se contínua, se os dados são primários (gerados pela própria empresa ou pesquisador) ou secundários (gerados por terceiros).
Apuração: Esta etapa serve para qualificar os dados e nela são feitas contagens, tabulações, agrupamentos e inserção em bancos de dados para o trabalho de análise.
Análise e interpretação: Nesta fase todo o ferramental estatístico entra em ação para analisar e descobrir as relações entre as variáveis buscando responder às hipóteses do problema de pesquisa. A geração de relatórios, apresentações e painéis (dashboards) fazem parte desta etapa e auxiliarão na tomada de decisão e na geração de conhecimento. A comunicação também é uma parte fundamental no final desta etapa pois, é através dela que o trabalho será melhor divulgado/vendido .
1.3 Como utilizar estatística?
Esta é uma pergunta vasta, mas com base em nossa experiência e na comunidade estatística, segue nove boas práticas para direcionar o pesquisador.
Estatística deve ser utilizada para ajudar a responder perguntas científicas: É importante inserir estatística desde o planejamento do experimento até a condução das análises e por fim a compilação dos conhecimentos adquiridos com base nos dados gerados pela pesquisa.
Pessoas se enganam. Dados não: Isso é verdade, mas tome cuidado, pois sinais sempre vêm com ruído. Por isso é fundamental entender muito bem o problema de pesquisa e conhecer seus dados para saber diferenciar dado bom de ruído. Questione as fontes e as formas que foram apresentadas.
Planejamento com foco no presente e no futuro: Este é um dos princípios mais violados nas ciências. Muitos só olham o aqui e agora e perdem muito tempo e dinheiro. portanto fique alerta. Fazer as perguntas certas e obter as respostas adequadas pode evitar perda de tempo, dinheiro e dores de cabeça na hora de analisar os dados obtidos de experimento mal planejados. Saiba a validade e sua pesquisa e dos seus dados e tenha em mente a replicabilidade. Se outros poderem chagar aos mesmos resultados será possível conferir robustez aos seus achados.
Atenção à qualidade dos dados: Se você tiver acesso ao processo de planejamento e coleta de dados seja cuidadoso e tenha em mente os impactos futuros na condução das análises. Dado ruim pode arruinar um estudo ou conduzir a resultados impróprios.

Figura 1.4: Anotei tudo
Estatística não é só técnica: Análise estatística é mais que um software. O software estatístico fornece ferramentas para auxiliar as análises, não para definílas-las. O contexto científico é crítico, e a chave para a análise estatística baseada em princípios é aproximar os métodos analíticos das questões científicas e de negócio.
Busque a simplicidade: As pessoas não gostam de complexidade. Uma boa parte dos modelos estatísticos exige formulação simples. Em muitos casos, uma simples análise descritiva resolve o problema. Tenha em mente que um grande número de medições, dados ausentes, erros, vieses de amostragem e outros fatores podem aumentar a complexidade do modelo e tornar o estudo impraticável.
Calcule a variabilidade: faz parte da análise estatística justamente ajudar a avaliar a incerteza, muitas vezes na forma de um erro padrão ou intervalo de confiança, e um dos grandes sucessos da modelagem estatística e inferência é que ela pode fornecer estimativas de erros padrão dos mesmos dados. Ao apresentar resultados, é essencial fornecer alguma noção de incerteza estatística envolvida em seu estudo.
Verifique as suposições das suas técnicas: É importante entender as suposições por trás dos métodos estatísticos e fazer o que for possível para entender e avaliar essas suposições. Não deixe que o software faça o papel do analista, ele apenas deve auxiliá-lo no processamento dos dados e nos cálculos. A validação das técnicas e as interpretações são sempre por conta do analista.
Torne seu trabalho reprodutível: Resultados replicáveis são fundamentais para que outros pesquisadores/analistas possam revisitar e reprocessar seus achados. Em muitos contextos, a replicação completa é muito difícil ou impossível, como em experimentos de larga escala, como ensaios clínicos multicêntricos, porém é sempre bom perseguir esta meta. Quando possível, forneça o conjunto de dados, juntamente com uma descrição completa da análise. Com isso deve ser possível reproduzir as tabelas, figuras e inferências estatísticas. Melhore drasticamente a capacidade de reproduzir descobertas sendo muito sistemático sobre as etapas da análise, compartilhando os dados e o código usados para produzir os resultados e seguindo as práticas recomendadas de estatística aceitas.
1.4 Como não utilizar estatística?
Aqui listamos também nove pontos de atenção para evitar mal uso da estatística.
Não minta com estatística: Alguns pesquisadores podem ser tentados a maquiar algum dados para seu benefício ou de outros. É sempre bom ter em mente que sua reputação e carreira podem estar em jogo ao apresentar falsos resultados. Sugerimos aqui uma leitura extra do livro do Darrell Huff, pois para não mentir é importante saber como se mente com estatística.
Resista aos mau intencionados: Se alguém te pediu pra fazer algo estatisticamente ilegal ou aplicar uma técnica inadequada, seja resistente e questione. Nem sempre o problema é simples, então é sempre bom ter uma compreensão da situação como um todo. Aprenda a dizer não para evitar problemas futuros.

Figura 1.5: Use a média
Cuidado com as suposições: É melhor assumir que não tem a resposta no momento e que a traz em outro momento do que inventar suposições incorretas só pra não sair por baixo em uma conversa. Ou pior, realizar um estudo/projeto apoiado por suposições incorretas sobre uma técnica estatística. Cedo ou tarde e você poderá se por em uma saia justa e ter de voltar atrás.
Evite ambiguidades: A comunicação estatística precisa ser clara. Em termos estatísticos não há espaço para meias verdades, pois são os dados falando.
Tenha certeza do que está falando: Não subestime seu público. É verdade que algumas pessoas não falam ou entendem bem o estatiquês, mas fique alerta, pois muitos são conhecedores desta ciência, então por vias das dúvidas é melhor saber o que você vai comunicar para evitar constrangimentos.
Não seja complexo demais nas suas análises e comunicações: Neste ponto seja ponderado, pois nem tudo que é simples é fácil e nem tudo que é difícil é complexo. Do planejamento à entrega é sempre bom ter seu trabalho revisado / acompanhado por outra pessoa de forma a identificar pontos de melhoria. A linguagem, sempre que possível deve ser de simples compreensão.
Maria vai com as outras: Muito cuidado. Não é porque todo mundo faz algo de um jeito que você pode assumir que é certo. Censo crítico faz toda a diferença na identificação deste tipo de fenômeno.
Cuidado como modelos automáticos: Modelos automatizados ou semi-automatizados podem às vezes gerar saídas inesperadas. “.. todos os modelos são errados, mas alguns são úteis. — George E. P. Box”. Com a popularização do machine learning muitas pessoas tendem a pensar que se colocar os dados no computador e passar o algoritmo tudo ficará pronto. Temos casos recentes de que isso é possível. Não vamos entrar no mérito, mas como já comentamos antes, a inteligência é do analista e saídas imprevistas podem ocorrer.
Não acredite apenas na estatística: A estatística é fundamental e sem ela nada podemos fazer com os dados, mas esteja sempre atento ao negócio ou qualquer evento externo que possa influenciar e alterar seus resultados.
1.5 Estatística, Data Science e Big Data.
Desde que o conceito de dado passou a existir, a estatística se faz presente. A seguir um pequeno texto que relaciona a estatística com Data Science e Big Data.
Estatística e Data Science (Ciência de Dados) são partes inseparáveis. De certa forma, a estatística é um subconjunto da ciência de dados. Mas o que é Data Science? É difícil definir um conceito tão amplo porém, a Wikipedia Norte Americana coloca da seguinte forma:
Data science, also known as data-driven science, is an interdisciplinary field about scientific methods, processes and systems to extract knowledge or insights from data in various forms, either structured or unstructured, similar to Knowledge Discovery in Databases (KDD). Fonte: https://www.wikiwand.com/en/Data_science, acesso em “08/12/2019”
No texto acima podemos isolar o termo interdisciplinary que remete a um conjunto de muitas áreas do conhecimento. Podemos marcar desta definição aos conceitos:
- Métodos Científicos - Métodos estatísticos e computacionais, por exemplo;
- Processos - Organização de passos para atingir um objetivo;
- Sistemas - Sistemas informatizados, por exemplo, são ferramentas superpoderosas para realizar Data Science.
Tudo com objetivo de obter conhecimento com base em dados, sejam eles estruturados ou não estruturados. Expandindo mais um pouco, pode-se incluir o termo Big Data que envolve dados estruturados ou não estruturados em grandes volumes. O conceito de Big Data também é complexo e discutível. (De Mauro, Greco, and Grimaldi 2016) propõem uma definição deste termo como segue.
Big Data is the Information asset characterized by such a High Volume, Velocity and Variety to require specific Technology and Analytical Methods for its transformation into Value.
Deixamos ao leitor interessado consultar (De Mauro, Greco, and Grimaldi 2016) para mais definições sobre Big Data.
Podemos isolar nesta definição os termos:
- Volume Alto - O termos alto pode ser relativo e depende do tipo de computador que está suportando a análise. Nós entendemos como volume alto qualquer base de dados que não pode ser processada por um sistema de tabulação como LibreOffice calc e seu concorrente da Microsoft;
- Velocidade - Grandes bases exigem processamento rápido e algorítimos rápidos muitas vezes são mais relevantes que um bom Hardware;
- Variedade - Bancos de dados de fontes diversas podem ser relacionados para obter conhecimento.
Estes termos chave estão direcionados diretamente com tecnologia e métodos estatísticos para transformar dados o obter valor ou seja, conhecimento. Aqui percebemos que Data Science, Big Data possuem muito em comum. Ambas utilizam dados como combustível visando descobrir novos conhecimentos. Ou seja, tudo isso precisa de estatística para fazer sentido.
Com base nos conceitos até aqui, poderíamos sugerir nossa própria definição de Data Science.
“Data Science é uma ciência ampla que une métodos científicos como a estatística, processos e sistemas tecnológicos buscando, através da análise de dados, sejam eles simples ou Big Data estruturados ou não, obter conhecimento acerca de fenômenos e processos variados”.
1.6 Conceitos e definições
A partir de agora iniciamos os estudos de estatística e para melhor compreender alguns conceitos, vamos trabalhar com o conjunto de dados da IES do Censo da Educação Superior no Brasil de 2017.
# Carregando pacote rnp
require(rnp, quietly = TRUE)
# Dados IES
base_ies <- rnp::dm_ies
# Tabela
base_ies %>%
dplyr::mutate(Sigla = SG_IES,
TotalTecnicos = QT_TEC_TOTAL,
ReceitaPropria = VL_RECEITA_PROPRIA,
DespesaPesquisa = VL_DESPESA_PESQUISA) %>%
dplyr::select(Sigla, TotalTecnicos, ReceitaPropria,DespesaPesquisa) %>%
head(n = 10) %>%
knitr::kable(digits = 2, align = "llrrr",
booktabs = TRUE, format = tb_formata,
caption = "Dez primeiras observações base de IES") %>%
kableExtra::kable_styling(latex_options = "hold_position")| Sigla | TotalTecnicos | ReceitaPropria | DespesaPesquisa |
|---|---|---|---|
| UFMT | 1574 | 6913132 | 5807924 |
| UNB | 3206 | 63239902 | 5772538 |
| UFS | 1429 | 3161937 | 3033336 |
| UFAM | 1721 | 4136205 | 1490991 |
| UFOP | 786 | 3458763 | 748715 |
| PUCPR | 1275 | 616991005 | 11948066 |
| UNICAP | 441 | 142785305 | 560400 |
| UCS | 986 | 338035351 | 3380182 |
| UNISINOS | 1062 | 487902230 | 6687713 |
| UCPEL | 246 | 100089191 | 3540465 |
Iniciamos aqui a revisão de alguns dos conceitos utilizados na linguagem estatística de forma simplificada. Isso nos ajudará a falar os termos e alguns jargões da linguagem estatística para enriquecer o diálogo.
1.6.1 População, amostra, censo
População: É o conjunto de todos os elementos (pessoas, animais, plantas, etc.) que possuam alguma característica de interesse.
Amostra: É um pedaço ou subconjunto da população e, a partir dela, faz-se inferência sobre as características da população. A ideia de amostra significativa vem do fato de que para representar a população, a amostra precisa preservar suas características.

Figura 1.6: População e amostra
Censo: É o processo utilizado para coletar dados abordando todos os elementos de uma população. Neste caso não há necessidade de amostras, pois toda a população é considerada.
Parâmetro: É qualquer medida numérica que serve para descrever uma característica de uma população. São geralmente representados por letras gregas. Por exemplo: média (\(\mu\)), variância (\(\sigma^2\)) e desvio padrão (\(\sigma\)).
Estatística: Tem a mesma função do parâmetro, porém é medido na amostra. São geralmente representados por letras latinas com acentos. Por exemplo: média amostral (\(\bar X\)), variância (\(S^2\)) e desvio padrão (\(S\)) amostrais.
1.6.2 Dados, informação, conhecimento e sabedoria
Dados: Dados são resultados de medições ou qualquer fonte relato documentado. Por si só dados não tem significado concreto porém, a disponibilidade dos mesmos é matéria prima para a obtenção de informações. Dados podem ser obtidos pela percepção através dos sentidos, pela execução de um processo de medição, por sensores, pesquisas, censos, etc.
Informação: O processamento e análise dos dados gera informação que auxilia a tomada de decisão seja nos negócios, pela ciência e na vida cotidiana em geral.
Conhecimento: O conhecimento extrapola a informação, ele produz ideias e experiências. Através do conhecimento é possível a abstração e a evolução de ideias e conceitos novos com base em todo tipo de experiência, sejam elas oriundas das informações ou vivências.
Sabedoria: Vai além do conhecimento e trata-se de um conhecimento extenso e profundo de várias coisas e suas relações com múltiplos eventos ou de um tópico em particular explorado ao extremo. Geralmente a sabedoria vem guiada por experiências práticas e vivências. Neste nível o conhecimento é extrapolado e visto de vários ângulos.
1.6.3 Variáveis
Variáveis são características medidas em cada elemento da amostra ou população. Elas podem ter valores numéricos ou não numéricos e seus valores podem varia de elemento para elemento.
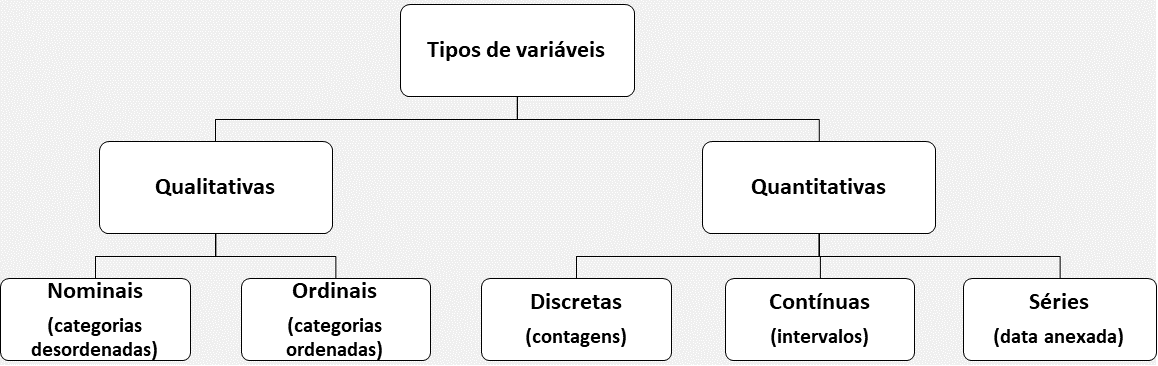
Figura 1.7: Tipos de variáveis
A figura 1.7 traz um resumo dos tipos mais comuns de variáveis. Detalhamos um pouco mais a seguir.
Variáveis qualitativas: As variáveis categóricas ou qualitativas descrevem caraterísticas dos indivíduos da amostra ou população. Elas podem ser nominais, quando descrevem características arbitrárias sem efeito de ordenação ou ordinais, quando descrevem relações de ordenação. A coluna
Siglada tabela 1.1 representa uma variável qualitativa nominal. Exemplos de ordinais sãoclasse socialeescolaridade.Variáveis quantitativas: As variáveis numéricas ou quantitativas se classificam em discretas e contínuas. As discretas representam contagens e as contínuas, medidas geralmente com casas decimais. Na tabela 1.1, a coluna
TotalTecnicosque representa o total de técnicos das IES é um bom exemplo de variável quantitativa discreta. Já as colunasReceitaPropria e DespesaPesquisasão variáveis contínuas, pois são medidas que representam valores de receita.Séries temporais: As variáveis quantitativas quando indexadas de uma variável de tempo, por exemplo hora, dia, mês, ano, etc. são classificadas como séries temporais. Séries temporais possuem um grande valor e por isso a estatística reserva um campo completo de estudos para este tipo de dado.
1.6.4 Análise univariada, bivariada e multivariada
A análise univariada: Busca-se descrever a população ou amostra analisando cada variável de forma isolada. É a maneira mais simples de obter informação e de fazer a estimativa estatística. Exemplos de análises univariadas são as médias, medianas e quatis.
A análise bivariada: Analisa relações existentes entre pares de variáveis para fins de explicação e/ou previsão. Na análise bivariada, a formulação de uma hipótese precisar ser feita e a estatística permitirá inferir ou confirmar esta hipótese. Análise de correção entre duas variáveis e tabelas de frequência de dupla entrada são exemplos de análise bivariada
A análise multivariada: Na análise multivariada a estatística dispões de uma série de técnicas que analisam de forma conjunta as múltiplas relações das variáveis. Regressão múltipla, análise de cluster e fatorial são exemplos de análises multivariadas.
1.6.5 tidydata
Em seu artigo, (Wickham and others 2014) discutem e mostram uma forma repensada de organizar tabelas estruturadas para análise de dados. De forma simples, um significado para tidy data é: dados arrumados, organizados.
Um conjunto de dados para ser tidy precisa ter três ingredientes:
- Cada observação é uma linha;
- Cada variável é uma coluna;
- Cada valor está em uma célula (linha x coluna);
Dados neste formato ajudam a tornar a análise mais rápida, principalmente com as ferramentas do tidyverso (Wickham 2017). A Tabela 1.1 mostra uma configuração de dados tidy, onde cada linha representa uma observação ou indivíduo que no caso é uma IES; cada coluna representa uma variável ou característica, por exemplo Sigla ou ReceitaPropria da IES e o cruzamento entre linhas e colunas são os valores correspondentes.
Observação: Nas empresas o conceito de tidy data geralmente é atribuído ao que chamam de ABT (Analytics Base Table). Este é o estado da arte que nem sempre é fácil de se chagar, mas uma vez lá, os dados estarão prontos para todo tipo de análise estatística e modelagem.
# Exemplos de tidydasets
knitr::kable(
list(head(mtcars[,1:4], 10), head(dplyr::starwars[,1:4], 10)),
booktabs = TRUE, format = tb_formata,
caption = "Amostra de outras tabelas de dados organizados") %>%
kableExtra::kable_styling(latex_options = "hold_position")
|
|
1.6.6 Exercícios resolvidos
Com apoio da base de IES, cuja amostra foi mostrada na tabela 1.1 vamos exercitar os conceitos vistos até agora.
- População e amostra
## [1] "2448 Universidades."paste("A base tem",
base_ies %>% transmute(TotalTecnicos = QT_TEC_TOTAL) %>%
filter(TotalTecnicos > 2000) %>%
nrow(), "IES com mais de 2000 técnicos")## [1] "A base tem 29 IES com mais de 2000 técnicos"- Dados, informação e conhecimento
- Variáveis e tipos de análises
rnp_atributos().
# Listando os atributos da base de ies para as 10 primeiras colunas
rnp::rnp_atributos(base_ies) %>%
head(n = 10) %>%
knitr::kable(booktabs = TRUE, format = tb_formata) %>%
kableExtra::kable_styling(latex_options = "hold_position")| classeBase | comprimento | variaveis | classeVars |
|---|---|---|---|
| data.table | 2448 linhas e 47 colunas | NU_ANO_CENSO | integer |
| data.table | 2448 linhas e 47 colunas | CO_IES | integer |
| data.table | 2448 linhas e 47 colunas | NO_IES | character |
| data.table | 2448 linhas e 47 colunas | SG_IES | character |
| data.table | 2448 linhas e 47 colunas | CO_MANTENEDORA | integer |
| data.table | 2448 linhas e 47 colunas | NO_MANTENEDORA | character |
| data.table | 2448 linhas e 47 colunas | CO_REGIAO | integer |
| data.table | 2448 linhas e 47 colunas | CO_UF | integer |
| data.table | 2448 linhas e 47 colunas | CO_MUNICIPIO | integer |
| data.table | 2448 linhas e 47 colunas | QT_TEC_TOTAL | integer |
Referências
De Mauro, Andrea, Marco Greco, and Michele Grimaldi. 2016. “A Formal Definition of Big Data Based on Its Essential Features.” Library Review 65 (3): 122–35.
Gil, Antonio Carlos. 2008. Métodos E Técnicas de Pesquisa Social. 6. ed. Ediitora Atlas SA.
Köche, José Carlos. 2016. Fundamentos de Metodologia Cientı́fica. Editora Vozes.
Montgomery, Douglas C. 2017. Design and Analysis of Experiments. John wiley & sons.
Wickham, Hadley. 2017. “Tidyverse: Easily Install and Load’tidyverse’packages.” R Package Version 1 (1).
Wickham, Hadley, and others. 2014. “Tidy Data.” Journal of Statistical Software 59 (10): 1–23.